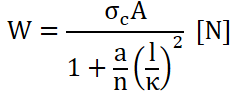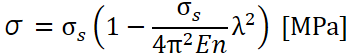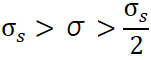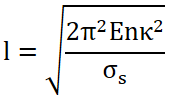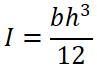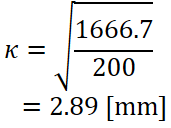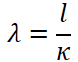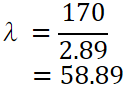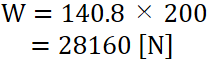【ジョンソンの式】座屈荷重の計算方法|アルミ等ランキンが使えないときの代用に
2023/02/05
機械設計において座屈荷重を計算するとき、オイラーの式とランキンの式が有名です。
比較的長い柱はオイラーの式、短い柱はランキンの式、という使い分けをするのですが、柱の材料によってはランキンの式が使えないときがあります。
そんな時に「ジョンソンの式」を使ってみては?という提案です。
計算例も載せていますので、この記事を読めばジョンソンの式で座屈強度が計算できるようになります。
ちなみにオイラーの式とランキンの式の計算方法は下記の記事で説明しています。
座屈以外の強度計算は下記の記事が参考になります。
この記事の目次
ランキンの式が使えない状況とは?
ランキンの式が使えないってどんな時?と思いますよね。
ちなみにランキンの式というのがこちらです。
定数aと圧縮応力σcは次の表から選択します。
| 定数\材料 | 軟鋼 | 硬鋼 | 鋳鉄 | 木材 |
|---|---|---|---|---|
| a | 1/7500 | 1/5000 | 1/1600 | 1/750 |
| σc | 330 | 480 | 550 | 50 |
お分かりでしょうか?
定数aと圧縮応力σcを表から選ばないといけません。
選ぶと言っても材料は「軟鋼」、「硬鋼」、「鋳鉄」、「木材」くらいしかなく、アルミとかステンレスとかないんですね。
圧縮応力は各材料のデータを調べたら分かるかもしれませんが、定数aが分かりません。
ランキンの式自体が、実験により求められた式だそうです。
未知の材料の定数aを求めるためには、実験をしないといけないってことですね。
そんな事は、一機械設計者としてはなかなか出来ません。
定数が分からないので、アルミとかステンレスとか、普通によく使われる材料すらランキンの式で計算できません。
困った。
ジョンソンの式なら定数がないのでアルミも計算できる
そこで登場するのがジョンソンの式。
材料力学の本にも載ってないことが多かったりします。
マイナーなのかな?
ランキンの式は計算に定数が必要でしたが、ジョンソンの式にはそのような定数はありません。
つまり、ジョンソンの式なら定数の不明なアルミやステンレスなどの材料であっても計算できるということです。
ただし、計算に必要なパラメーターとして縦弾性係数、降伏圧縮応力の値が必要です。
これらは一般的な材料であれば、調べたら分かることが多いです。
ジョンソンの式の計算方法
ジョンソンの式の公式はこちらになります。
| σ(シグマ) | 座屈応力 [MPa] |
|---|---|
| σS | 降伏圧縮応力 [MPa] |
| π(パイ) | 円周率 |
| E | 縦弾性係数 [MPa] |
| n | 端末係数 |
| λ(ラムダ) | 細長比 |
各値に具体的な数値を代入して計算したら座屈応力が求まります。
縦弾性係数 Eや降伏圧縮応力 σSは材料に固有の値なので、文献やネットで調べたらOKですが、端末係数 nや細長比 λについては計算したり確認する必要があります。
細長比の求め方
次の手順で計算しますが、断面形状によって断面二次モーメントを求める式が違うので注意しましょう。
- 断面形状、寸法より「断面積」と「断面二次モーメント」を計算
- 断面積と断面二次モーメントより「断面二次半径」を計算
- 断面二次半径と柱の長さより「細長比」を計算
細長比の求め方については、以下の記事で詳しく説明していますのでよろしければご覧ください。
端末の条件より「端末係数」を確認する
柱の端末(上端と下端)の条件により、端末係数が決まります。
計算したい柱が下の表のどれに当てはまるか確認して端末係数を決定します。
| 端末条件 | 自由端 | 両端回転端 | 回転端固定端 | 両端固定端 |
|---|---|---|---|---|
| 曲がり方 |  |
 |
 |
 |
| 端末係数 | n=1/4 | n=1 | n=2 | N=4 |
座屈荷重は、座屈応力×断面積
縦弾性係数 Eや細長比 λ等の各パラメータをジョンソンの式に代入して計算すると座屈応力が計算できます。
座屈応力は単位面積あたりの荷重です。
その柱にいくらの荷重をかけたら座屈するのかを求めるには「座屈荷重」を求める必要があります。
座屈荷重を計算するには、座屈応力 × 断面積としてやります。
降伏圧縮応力をいくらにする?
ジョンソンの式の計算には縦弾性係数 Eと降伏圧縮応力 σsの値が必要です。
縦弾性係数はちょっと調べたら分かることでしょう。
問題は降伏圧縮応力。
JISで規定されている鋼材の降伏点は通常は「引張」の降伏点です。
圧縮の降伏点は規定されていません。
しかし一般的な金属材料は引張と圧縮の強度は同程度と考えて概ね問題ないため、ジョンソンの式の計算の圧縮降伏応力には材料の降伏点の値を用いればよいでしょう。
アルミなどの降伏点が明確に現れない材料の場合は0.2%耐力の値を用います。
以下に主な材料の縦弾性係数と降伏点を記します。
参考値なので、実際の設計時にはJIS等できちんと調べることをおすすめします。
| 材質 | 縦弾性係数 E [Mpa(N/mm2)] | 降伏点、耐力 [MPa(N/mm2)] |
|---|---|---|
| 軟鋼 | 206,000 | 235 |
| 鋼 | 216,000 | 345 |
| ステンレス(SUS304) | 186,000 | 205 |
| リン青銅 | 120,000 | 392 |
| アルミニウム(A5052) | 72,000 | 65 |
| 銅(C1100) | 118,000 | 69 |
ジョンソンの式の適用範囲
オイラーの式にも適用範囲出来る範囲があるように、ジョンソンの式にも適用できる範囲が決まっています。
その範囲外でジョンソンの式を使ってしまうと、とんでもない結果になってしまいます。(座屈応力がマイナスになったりする)
ジョンソンの式が使える範囲がこちら。
| σ(シグマ) | 座屈応力 [MPa] |
|---|---|
| σS | 降伏圧縮応力 [MPa] |
ジョンソンの式で計算した座屈応力σが、降伏圧縮応力σSの半分(σS / 2)より大きいときに適用となります。
ちなみにジョンソンの式で計算した座屈応力σは降伏圧縮応力σSを絶対に超えないので、σS > σについては気にしなくて大丈夫です。
でもこの式だと、座屈応力を計算してみないとジョンソンの式が適用なのか、そうじゃないのか分かりませんね。
境界となる長さを知りたいときは、ジョンソンの式にσ=σS/2を代入して、柱の長さlについて変形した次の式で計算できます。
| l (小文字のエル) | 柱の長さ[mm] |
|---|---|
| π(パイ) | 円周率 |
| E | 縦弾性係数 [MPa] |
| n | 端末係数 |
| κ (カッパ) | 断面二次半径 [mm] |
| σS | 降伏圧縮応力 [MPa] |
ジョンソンの式の計算例
次の例でジョンソンの式に具体的な数値をいれて座屈応力を計算してみましょう。
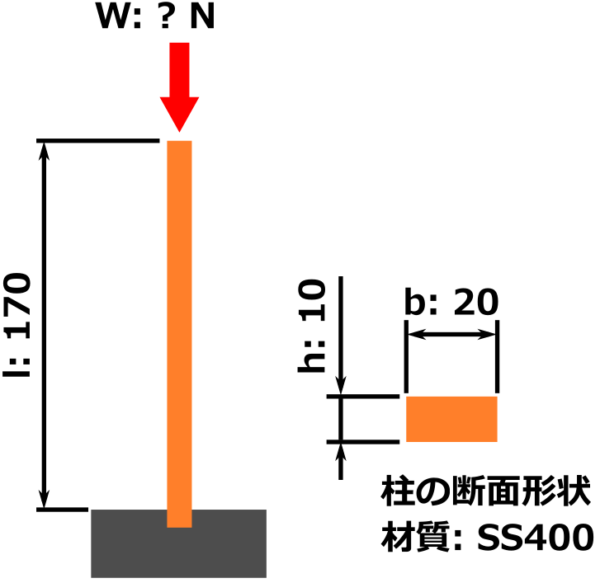
- 部品の断面は 幅20 mm、高さ10 mmの長方形
- 柱の長さ170mm
- 柱の根本は地面に固定、上端は固定されてない自由端
- 材質:SS400
適用されるのはジョンソンの式?オイラーの式?
ジョンソンの式は比較的短い柱に適用され、長い柱はオイラーの式で計算するという使い分けをします。
計算したい柱に適用されるのがジョンソンの式かオイラーの式になるのか、先に確認しておきましょう。
| l (小文字のエル) | 柱の長さ[mm] |
|---|---|
| π(パイ) | 円周率 |
| E | 縦弾性係数 [MPa] |
| n | 端末係数 |
| κ (カッパ) | 断面二次半径 [mm] |
| σS | 降伏圧縮応力 [MPa] |
上の式に各パラメータを代入して計算すればジョンソン or オイラーの境界となる長さが分かります。
縦弾性係数 Eや降伏圧縮応力 σSは材料固有の値を調べて入れてやればOK。
しかし断面二次半径を先に計算しないといけません。
断面二次半径の計算
断面二次半径の計算方法の詳細は以下の記事でも紹介していますが、今回の例で実際に計算してみます。
まず断面積の計算。
今回計算する例では、
b = 20 [mm]
h = 10 [mm]
なので、以下計算の通り断面積は200 mm2です。
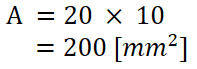
次に最小断面二次モーメントの計算をします。
数値を公式に代入して計算すると、断面二次モーメントは1666.7 mm4となりました。
断面積と最小断面二次モーメントが計算できたので、最小断面二次半径を計算出来ます。
今回の例では最小断面二次モーメントIが3333.3 mm4、断面積が400 mm2だったので公式に代入して計算します。
計算により断面二次半径κは2.89 mmということが分かりました。
ジョンソンの式の適用範囲の境界の長さを計算する
断面二次半径が計算できたところで、改めてジョンソンの式の適用範囲の境界の長さを計算していきましょう。
| l (小文字のエル) | 柱の長さ[mm] |
|---|---|
| π(パイ) | 円周率 |
| E | 縦弾性係数 [MPa] |
| n | 端末係数 |
| κ (カッパ) | 断面二次半径 [mm] |
| σS | 降伏圧縮応力 [MPa] |
式に代入するパラメーターは以下の通りです。
| l (小文字のエル): 柱の長さ | 170 [mm] |
|---|---|
| π(パイ): 円周率 | 3.14・・・ |
| E: 縦弾性係数 | 206,000 [MPa] |
| n: 端末係数 | 0.25 |
| κ (カッパ): 断面二次半径 | 2.89 [mm] |
| σS: 降伏圧縮応力 | 235 [MPa] |
式に代入して計算します。
計算の結果、190mmより長いとオイラーの式、短いとジョンソンの式が適用となることがわかりました。
今回の例の柱の長さは170mmなので、ジョンソンの式が適用となります。
ジョンソンの式で座屈強度を計算する
次のジョンソンの式を用いて計算しますが、細長比 λ(ラムダ)と端末係数 nが不明なので先に確認しておきましょう。
細長比を計算する
今回の例は柱の長さlが170 mm、最小断面維持半径κは先程すでに計算済みで2.89 mmでしたね。
細長比の式に代入して計算すると、細長比λは58.89と分かりました。
端末係数を確認
今回の例は下端が固定で上端が自由端なので、次の表より端末係数は「1/4 (0.25)」となります。
| 端末条件 | 自由端 | 両端回転端 | 回転端固定端 | 両端固定端 |
|---|---|---|---|---|
| 曲がり方 |  |
 |
 |
 |
| 端末係数 | n=1/4 | n=1 | n=2 | N=4 |
ジョンソンの式の計算
計算に必要な細長比と端末係数が確認出来たところで、いよいよジョンソンの式の計算をしてみましょう。
座屈の計算は、座屈の公式を使うまでの下準備がちょっと長いですよね。
式に代入するパラメータをまとめると以下になります。
| σS: 降伏圧縮応力 | 235 [MPa] |
|---|---|
| π(パイ): 円周率 | 3.14・・・ |
| E: 縦弾性係数 | 206000 [MPa] |
| n: 端末係数 | 0.25 |
| λ(ラムダ): 細長比 | 58.89 |
公式に代入していきます。

というわけで、座屈応力(座屈強さ)は140.8 MPaという計算結果になりました。
座屈荷重も求めてみます。
座屈応力×断面積で座屈荷重が計算できます。
この柱は28160 Nの荷重をかけると座屈することが分かります。
仮に安全率を5とすると、28160 / 5 = 5632 [N]まで荷重をかけられることになります。
グラフで比較、ジョンソン、ランキン、オイラーの式の計算結果
長い柱はオイラーの式で計算し、一定以下の短い柱はランキンの式で計算する、と参考書ではよく紹介されています。
でもこれ、オイラーとランキンの選択の境界付近で長さを検討しているときにちょっと問題があります。
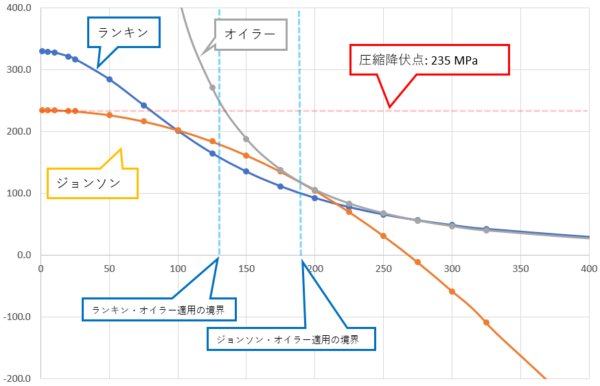
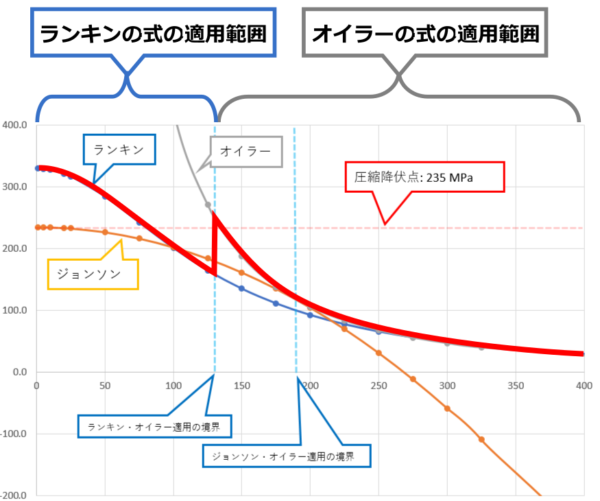
まずはこちらのグラフをご覧ください。
今回、ジョンソンの式で計算した例をオイラーの式、ランキンの式、ジョンソンの式でそれぞれ計算した結果をグラフ化したものです。
横軸が柱の長さ [mm]、縦軸が座屈応力 [MPa]となっています。
このグラフを眺めてみるとなかなか興味深いですね。
オイラーの式は、柱の長さが0に近づくと、座屈応力が無限に大きくなっていきます。
オイラーの式を短い柱に適用できない理由がこれですね。
実際には圧縮により破壊されてしまいますが、オイラーの式は曲げによる破壊しか考慮しないので、座屈応力が無限に大きくなります。
ランキンの式は柱の長さが0のときの座屈応力が、材質により決められた圧縮応力となっています。
ジョンソンの式は柱の長さが0のときの座屈応力が圧縮降伏応力となり、柱が長くなるとなんと座屈応力がマイナスになってしまいます。
現実にはマイナスになるワケはなく、ジョンソンの式の適用範囲が以下の範囲となります。
| σ(シグマ) | 座屈応力 [MPa] |
|---|---|
| σS | 降伏圧縮応力 [MPa] |
この「σ = σS / 2」」のときにオイラーの式とジョンソンの式の計算結果の曲線が接します。
オイラーの式とランキンの式を適用したときの問題点
長い柱をオイラーの式、短い柱をランキンの式で計算しようとすると、計算結果は下のグラフの赤いラインとなります。
柱の長さが130 mm付近にオイラー、ランキンの式の適用の境界があり、柱をどんどん短くしていくと座屈応力は高くなっていき、適用する式がランキンの式に切り替わった瞬間にストンと座屈応力が下がります。
計算ではそうなるんですが、現実の現象としてはおかしいですよね。
この例で柱の長さ130mm付近で設計を検討していると、うまく判断できなくて困ってしまいますね。
オイラーの式とジョンソンの式を適用した場合
次に、下のグラフの赤いラインは長い柱をオイラーの式、短い柱をジョンソンの式で計算したときの結果です。
「σ = σS / 2」のときにオイラーの式とジョンソンの式の計算結果の曲線が接し、ジョンソン、オイラーどちらを適用するかの境界となりますが、それが柱の長さ190 mm付近。
オイラーの式とジョンソンの式の計算結果はなめらかに繋がり、式選択の境界付近で長さを検討していたとしても、それほど違和感がないんじゃなでしょうか?
結局どの式を選択すれば良い?
実際に作ったものが壊れるかどうかももちろん重要ですが、DR等で誰かにもっともらしい説明をしないといけない、という事情もあると思います。
どの式を選択するかの例として、次のような考え方もできます。
- 特に問題なければ一番一般的と思われるオイラーの式とランキンの式を用いる。
- 式選択の境界付近での座屈応力に違和感が少なくしたいときはオイラーの式とジョンソンの式を。
- 安全性が最優先で適用可能な式が複数ある場合、最も座屈応力の小さい式を選択
上記のような理由でこの式を選択したと説明出来れば、相手にも納得してもらいやすいんじゃないでしょうか。
ちなみにこの他にも「テトマイヤーの式」というのもあります。
興味があれば調べてみてください。
まとめ
ランキンの式が使えないとき、ジョンソンの式で代用できる可能性があります。
座屈以外の強度計算は下記の記事が参考になります。