部品にせん断荷重が加わった場合に発生するせん断応力、部品は壊れないか、どれほどの荷重で破壊されるのか、と言った機械設計における強度計算方法を説明します。
せん断以外の強度計算は下記の記事が参考になります。
せん断応力によりどれだけ滑り変形するかの計算は下記の記事が参考になります。
機械設計技術者が転職する方法まとめ
この記事の目次
何Nでせん断破壊する?
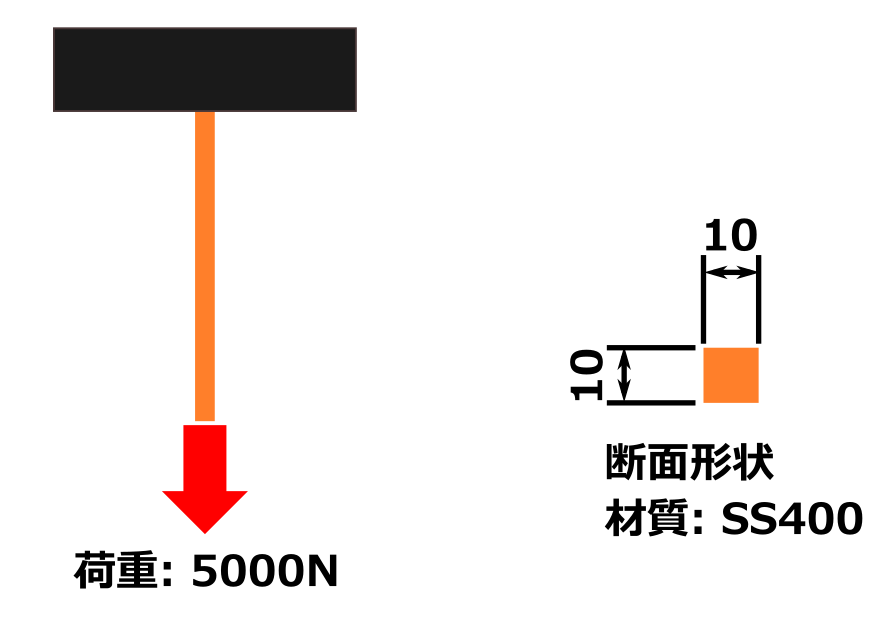
今回、例題として強度を確認したいのはオレンジ色の部品。
黒い壁に棒状のオレンジの部品が固定されています。
ここに青色のとても重い物体が乗っていて、オレンジに5000 Nの荷重がかかっています。
この図のような状況のとき、オレンジ色の部品は壊れるのか壊れないのか?
またどのくらいの力で壊れるのか?ということを計算したいと思います。
- 部品の断面は 10 mm × 10 mmの正方形
- 材質:SS400
- 5000Nのせん断荷重がかかる
という条件です。
せん断荷重とは?
そもそもせん断って何?って人もいると思います。
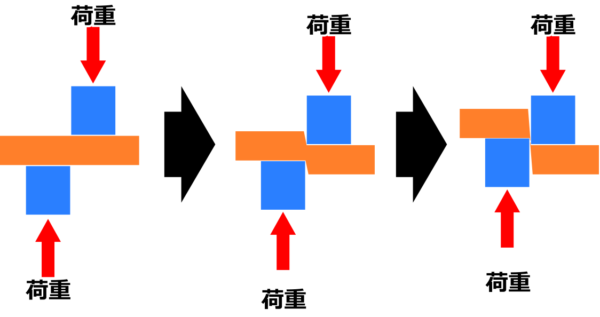
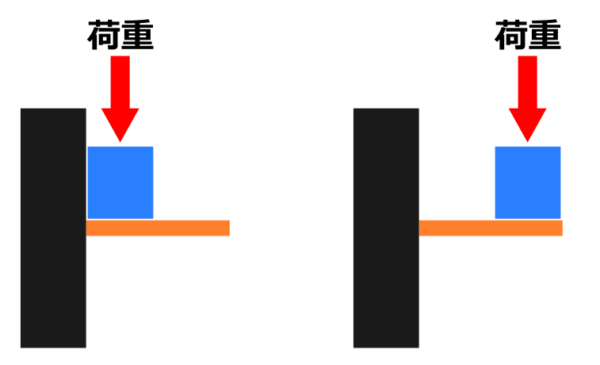
せん断荷重とはこのような荷重のことです。
ハサミで紙を切ったり、プレスで鉄板に穴を打ち抜いたりするのもせん断による加工となります。

図の中央の例は、まさにハサミで紙を切るイメージですね。
図の右の例は、2枚の板の穴に通した軸にせん断荷重がかかっているイメージ。
ボルトで板を締結したとき、板が滑るとこのようにせん断荷重が加わります。
このように板(や軸)の面に垂直に作用する方向に荷重が加わると、板の左右の部分が荷重の方向に滑ろうとします。
このような荷重を「せん断荷重」と呼びます。
せん断応力とは?
「せん断荷重」とは部品等の材料に外部から働く力のことですが、「せん断応力」とは何なのでしょうか?
せん断応力とは、せん断荷重を受けた材料の内部に発生する、断面に沿った方向に抵抗する力のことです。
材料内部に生じたせん断応力が、材料の持つせん断強さを超えると、材料はせん断破壊されます。
部材に対する外部からの荷重を「外力」と呼ぶこともあり、それに対して応力は「内力」とも呼びます。
応力には大きく分けて2種類あります。
-
- 引張荷重や圧縮荷重に対する「垂直応力」
- せん断荷重やねじり荷重に対する「せん断応力」
計算方法は後ほど詳しく説明しますが、荷重が同じであれば断面積が大きいほど材料内部に生じる力である「応力」は小さくなります。
つまり、「部品が太くなれば強くなる」と言う、感覚的に当たり前のことが計算により表せるわけです。
せん断に対する強度計算の概要
今回の強度計算は次のステップで求められます。
- 強度計算したい部品の断面積と荷重よりせん断応力を求める
- せん断応力が材料のせん断強さ(引張強さ×0.6)より大きければ壊れる、小さければ壊れないと判断する
せん断応力の計算方法
それでは具体的に計算してみましょう。
せん断応力の公式
| τ(タウ) | せん断応力 [MPa] |
| W | 荷重 [N] |
| A | 断面積 [mm2] |
図より、荷重は5000 Nですが断面積が不明なので計算します。
1辺10mmの正方形なので、以下の通り断面積は100 mm^2です。
10 × 10 = 100 [mm2]
先程の公式に当てはめると以下の計算の通り発生するせん断応力は50 MPaとなります。
※ここで求めているのは正確には「平均せん断応力」といいます。
実際には部材の断面に均一に50 MPaの応力が発生するわけではなく、中央部が大きく、縁に行くにつれ応力は小さくなります。
断面中に発生する一番大きい応力を「最大せん断応力」と呼び、平均せん断応力よりも大きな値となります。
より正確に計算する場合は最大せん断応力を求める必要があります。
最大せん断応力の計算については、下記の記事で説明しています。
せん断強さは引張強さ×0.6とする
部材内に発生したせん断応力が材料のせん断強さを超えると破壊しますが、せん断強さはいくらなのでしょうか?
引張応力が発生しているときは、引張強さと比較すればよいですが、せん断の場合は?
一般的な金属の場合、せん断強さは下記の数値を用いればOKです。
せん断強さ = 引張強さ×0.6
この0.6という数値がどこから来たかというと、ミーゼスの降伏条件式より
せん断強さ = 引張強さ / √3
が導かれます。
1 / √3 = 0.57735
となり、0.6と近似となります。
今回の例の材質はSS400という軟鋼で、引張強さが400 MPaとなります。
先程の式に当てはめると、せん断強さは240 MPaです。
せん断強さ = 400 × 0.6
= 240 [MPa]
せん断応力とせん断強さを比較する
部品に発生するせん断応力と材料のせん断強さを比較し、
- せん断強さ > 部材のせん断応力 → 破壊しない
- せん断強さ < 部材のせん断応力 → 破壊される
と判断できます。
先程の計算結果より
せん断強さ: 240 [MPa] > 材料に発生するせん断応力: 50 [MPa]
となり、材料は破壊しないことが分かります。
ちなみに何Nの荷重でこの部品がせん断破壊されるかと言うと、まずせん断応力の公式を荷重Wを求める形に変形します。
W = τA
W [N] = 240 [MPa] × 100 [mm2]
= 24000 {N]
となり、24000 N (24 kN)でせん断破壊することになります。
ざっくり2.4 t(トン)くらいの物体が乗っかると壊れるということですね。
各材料の「引張強さ」と「せん断強さ」
強度計算に使用するための、いくつかの金属材料の「降伏点または耐力」、「引張強さ」と「降伏せん断強さ」、「極限せん断強さ」をまとめてみました。
降伏点・引張強さ×0.6を降伏せん断強さ・極限せん断強さとしています。
せん断応力が極限せん断強さを超えると材料は完全に破断、降伏せん断強さを超えると破断しないまでも永久変形が残る、と考えられます。
※あくまで目安です。この数値が正しい保証はないのでしっかり調べてから設計してくださいね。
| 種類 | 記号 | 降伏点または耐力 N/mm2 (= MPa) | 引張強さ N/mm2 (= MPa) | 降伏せん断強さN/mm2 (= MPa) | 極限せん断強さN/mm2 (= MPa) |
|---|---|---|---|---|---|
| 一般構造用圧延鋼 | SS400 | 245 | 400~510 | 147 | 240~306 |
| 機械構造用炭素鋼 | S45C | 345 | 570 | 207 | 342 |
| 機械構造用合金鋼 | SCM435 | 785以上 | 930以上 | 471以上 | 558以上 |
| ステンレス | SUS304 | 205 | 520 | 123 | 312 |
| ステンレス | SUS430 | 205 | 420 | 123 | 252 |
| アルミ合金 | A5052(質別: O) | 65 | 170~215 | 39 | 102~129 |
| アルミ合金(超々ジュラルミン) | A7075(質別: T6) | 240~460 | 360~545 | 144~276 | 216~327 |
| タフピッチ銅 | C1100(質別: O) | 69以上 | 195以上 | 41.4以上 | 117以上 |
| 黄銅 | C2801 | – | 325~470以上 | – | 195~282以上 |
他に、機械設計製図便覧にも材料の強弱表としてせん断の極限強さの記載があるので抜粋して紹介します。
上の表よりはずっとあてになると思います。
| 材料 | 極限強さ・引張 N/mm2 (= MPa) | 極限強さ・せん断 N/mm2 (= MPa) |
|---|---|---|
| 錬鉄(繊維に平行) | 320~370 | 250~320 |
| 軟鋼 | 330~440 | 280~370 |
| 鋼 | 440~880 | >400 |
| 鋳鉄 | 120~235 | 130~250 |
| 鋳鋼 | 350 | 390 |
| 黄銅 | 150 | 150 |
または、JIS B8265「圧力容器の構造-一般事項 」の4.3.2項にこのような記述があります。
「設計温度における材料の許容せん断応力は許容引張応力の0.8倍とする。」
これに則れば0.8倍でもOKとなりますね。
より安全側で考えるなら0.6倍となりますが、どれを採用するかは設計者次第です。
安全率を考慮して許容応力を決める
SS400の極限せん断強さが240 MPaとして、設計した部品に発生する応力が230 MPaだったとします。
極限せん断強さ: 240 MPa > せん断応力: 230 MPa
せん断応力は極限せん断強さ以下だからOK!というわけにはいきません。
強度がギリギリの設計だと、想定外の外力が少し加えられただけでも壊れる可能性があります。
そこで極限強さに「安全率」を掛けて許容応力を決定します。
破壊する応力に対して、許容する応力の余裕を何倍とるか、ということです。
安全率の公式は以下です。
| S | 安全率 |
| σ_B | 極限強さ [MPa] |
| σ_a | 許容応力 [MPa] |
極限強さと安全率から許容応力を求めるように変形するとこうなります。
安全率をいくらにするか、というのも諸説ありますが、簡便に用いられているのが下表の「アンウィンの安全率」。
| 材料 | 固定荷重 | 繰返し荷重(片振り) | 交番荷重(両振り) | 衝撃荷重 |
|---|---|---|---|---|
| 鋳鉄 | 4 | 6 | 10 | 15 |
| 軟鋼 | 3 | 5 | 8 | 12 |
| 鋳鋼 | 3 | 5 | 8 | 15 |
| 銅および合金 | 5 | 6 | 9 | 15 |
| 木材 | 7 | 10 | 15 | 20 |
| 石材・コンクリート | 20 | 30 | (25) | (30) |
荷重の種類や材料によって安全率が変わってきます。
例えば材質がSS400の場合は上の表では「軟鋼」に該当し、固定荷重の場合は安全率が「3」となります。
先程の公式に当てはめると以下の計算により許容応力は80 MPaとなります。
部品に発生する応力が80 MPa以下になるように部品の断面積を調整するなど、設計に反映します。
「SS400の許容応力は○○MPa」と言った一般的に決まった値はありません。
想定される荷重の種類、材質を考慮して設計者が許容応力を決めます。
仕様や社内の規格で決まっている場合はそちらに従いましょう。
許容応力のより詳しい求め方については下記記事で説明しています。
なぜせん断応力を求めるのか?
強度計算で部材に加わるせん断荷重を断面積で割ってせん断応力を求めました。
なぜわざわざせん断応力を求めるのでしょうか?
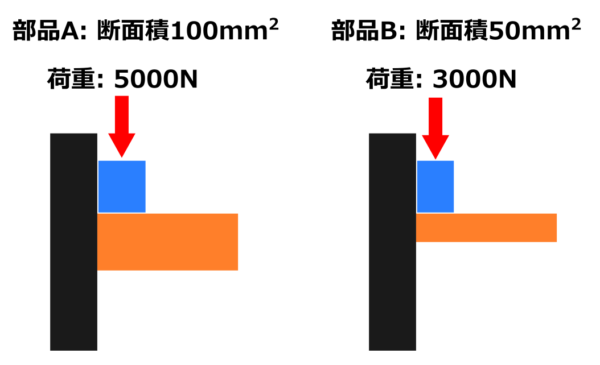
上の図のように部品Aと部品Bにせん断荷重がかかっているとして、部品Aの断面積は100 mm2に荷重5000 N、部品Bの断面積は50 mm2に荷重3000 Nだったとします。
この2つのパターンでどっちが部品が壊れやすいのか、パッと見ただけでは分からないですよね。
部品Aと部品Bの壊れやすさはどの程度違うのかを比較するために単位面積当たりの荷重、つまり応力を計算するわけです。
この例を計算してみると、部品Aに発生する応力は50 MPa。
σ = 5000 / 100
= 50 [MPa]
一方部品Bに発生する応力は60 MPa。
σ = 3000 / 50
= 60 [MPa]
部品Bに発生するせん断応力が少しですが大きくなっており、荷重は小さいですが部品Bのほうが強度的には厳しいということが分かります。
このように、断面積が異なると一概に荷重だけを見て判断できないため、強度計算の際には応力で考えるわけです。
せん断で破壊するか曲げで破壊するか?
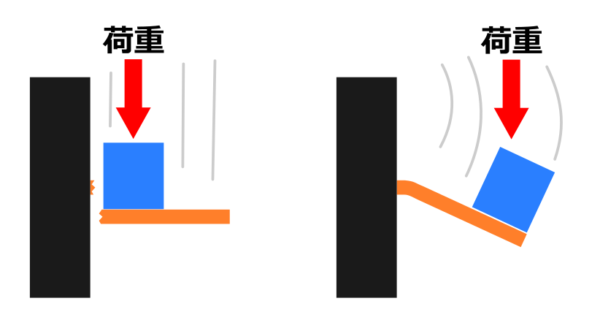
下の図のように、部材の根本または先端に荷重がかかっているとします。
荷重の位置以外は、オレンジ色の部材の寸法や荷重の大きさなどの条件は同じです。
荷重をどんどん増やしていったとき、左はせん断によって破壊しそうですが、右の場合はどうでしょうか?
右の場合は、せん断によって破壊するよりも先に、根本から曲がって変形しそうだと感覚的に分かりますよね。
このように、せん断による影響のみを考え曲げによる影響を考慮していない場合、作ったものがすぐに壊れた!となりかねません。
形状と荷重のかかり方から、どのような応力が発生するかをイメージして適切な計算ができるようになりたいですね。
ちなみに機械設計の現場では、上図の右の状況ではせん断応力はいちいち計算せず、曲げ応力のみ計算します。
判断できない場合は両方計算してももちろんOKです。
まとめ
せん断強度は次のように計算できます。
- 強度計算したい部品の断面積と荷重よりせん断応力を求める
- せん断応力が材料のせん断強さ(引張強さ×0.6)より大きければ壊れる、小さければ壊れないと判断する
さらに安全率を加味して部品サイズを決定すればOKです。
せん断以外の強度計算は下記の記事が参考になります。
機械設計技術者が転職する方法まとめ



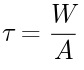

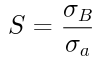
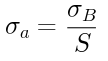


コメント
非常に勉強になる記事を掲載していただき、まことにありがとうございます。
材料のせん断強度が調査さ?れた文献や実験データはどこかに公開されてますでしょうか?
(例.SS400 S25C S45C SUS304などの材質)
また、これらの材質が選定されている機械の強度計算で、せん断強度が引張強度の60%程度に設定されている事例等はご存じですか?
コメントありがとうございます!
せん断強度が引張強度の60%程度に設定された実際の例は分かりませんが、
JIS規格のB8265圧力容器の構造-一般事項に各種材料の許容応力が記されており、4.3.2項に「せん断応力は許容引張応力の0.8倍」とするとされています。
(0.6倍じゃなく、ここでは0.8倍とされています)
また建築基準法で鉄鋼部材のせん断は1/√3 (≒0.6倍)とすると定められているようです。
なのでこの記事の「せん断強さ=引張強さ×0.6」とするのは考え方の一つであり、これが絶対正解じゃないですね。
0.8倍と0.6倍では、0.6倍を採用したほうがより安全側なので、迷ったらこちらにする、位の雰囲気です。
機械的性質の調べ方について以下の記事にまとめてますので、参考になれば。
「【材料力学】各材料の機械的性質の調べ方(引張強さ・降伏点(耐力)・弾性係数など)」
https://kawahara-zakki.com/how-to-check-material-strength/