断面形状が円(中実円)の丸棒、パイプ状(中空円)の軸にトルクがかかっている時、発生している応力がいくらなのか、どれほどのトルクをかけると破壊するかの計算方法について説明します。
これを読めば、ねじり応力の計算と、軸が破壊または永久変形するかの判断が出来るようになります。
ねじり以外の強度計算は下記の記事が参考になります。
ねじれ角(ねじり変形量)の計算方法は下記の記事で説明しています。
この記事の目次
軸のねじりの計算例題
直径10 mm、長さ 100mmの中身の詰まった丸棒(中実軸)の先端の中心から50 mmの位置に1000 Nの荷重がかかっています。
ねじりによるせん断応力はいくらでしょう?
材質は軟鋼(SS400)です。
(このケースでは荷重はねじりだけじゃなく軸を曲げる方にも作用しますが、曲げについては考慮しないことにします。)
計算方法を説明した後、実際に計算してみます。
軸をねじるとせん断応力が発生する
軸をねじったときにどのように破壊するかですが、ねじることにより部材内部にせん断応力が発生し、材料のせん断強さを超えると破壊します。
材料に加わる力の種類と部材内部に生じる応力の種類をまとめてみます。
| 力の作用の仕方 | 応力の種類 |
|---|---|
| 引っ張り or 圧縮 | 引張、圧縮応力 |
| 曲げ | 引張、圧縮応力 |
| せん断 | せん断応力 |
| ねじり | せん断応力 |
「引張(圧縮)」と「曲げ」の関係は、「せん断」と「ねじり」の関係によく似ています。
発生する応力の種類もそうですが、計算方法についても「曲げ」と「ねじり」は似たような式になっています。
ちなみに木材のように横断面より縦断面が弱い材料の場合は、ねじると縦方向に亀裂が入ります。
鋳鉄のようにせん断よりも引っ張りの方が弱い材料の場合は斜め45°の角度で割れます。
「せん断応力の共役性」が関係してくるのですが、詳細は割愛します。
ねじり応力計算の全体像
ねじり応力の計算は次のステップで出来ます。
- ねじりモーメント(トルク)を計算する
- 断面二次極モーメントを計算する(省略可能)
- 極断面係数を計算する
- ねじりの公式でせん断応力を計算する
下の画像は中身の詰まった中実円断面の場合です。
中空のパイプの場合は極断面係数の計算式が若干異なります。
| T | ねじりモーメント(トルク) [N・mm] |
|---|---|
| r | 中心から荷重の距離 [mm] |
| W | 荷重 [N] |
| ZP | 極断面係数 [mm3] |
| π(パイ) | 円周率 |
| d | 軸の直径 [mm] |
| τ(タウ) | せん断応力 [MPa] |
式に長さが入ってないことから分かるように、ねじりモーメントにより軸が破壊するかに軸の長さは無関係ということが分かります。
別の記事で説明しようと思いますが、軸の長さはどれだけの角度ねじれるかに関わってきます。
ねじり応力(せん断応力)の計算方法の詳細
では、計算方法の詳細について順を追って説明していきます。
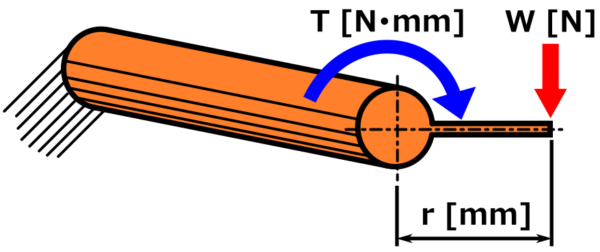
ねじりモーメント(トルク)の計算
軸にかかる荷重と、荷重の位置よりねじりモーメント(トルク)を計算します。
加わるトルクが最初からわかっている場合は、計算する必要はもちろんありません。
次の2パターンの計算方法を示していますので、状況に応じて計算してください。
荷重が1箇所の場合
中心からの距離 r [mm]の位置に荷重 W [N]がかかっている例。
荷重と中心からの距離を掛け算することでトルクを求められます。
スパナでボルトを締めるようなイメージです。
荷重が中心を挟んで2箇所の場合
2箇所に向かい合うように荷重 W [N]がかかっていて、荷重と荷重の距離が l [mm]のパターン。
荷重と荷重間の距離を掛け算することでトルクを求められます。
距離 lは半径ではなく荷重と荷重間の距離であることに注意してください。
T型のスパナやハンドルを両手で回すようなイメージです。
トルクの単位としては N・mの方が(ニュートン・メートル)のほうが一般的かもしれませんが、今回の説明ではトルクの単位を N・mm(ニュートン・ミリメートル)で計算しています。
N・m = N・mm / 1000
で換算できます。
断面二次極モーメントを計算する(省略可能)
極断面係数を計算するために「断面二次極モーメント」を計算するんですが、お急ぎの方は飛ばして次の「極断面係数の計算」に進んでもらってOKです。
目的がせん断応力を求めるだけであれば、わざわざ断面二次極モーメントを計算しなくても、極断面係数の式を使えば済むからです。
一応知っときたい人のために断面二次極モーメントの計算について説明しますね。
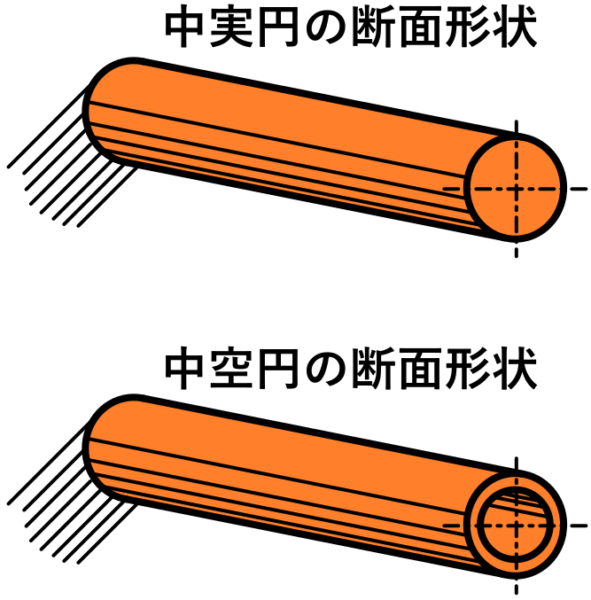
まず用語の説明ですが、中身の詰まった丸棒の断面形状を「中実円」、パイプ状の断面形状を「中空円」と呼ぶので覚えといてください。
「断面二次極モーメント」に似た言葉に、曲げ応力の計算等で使う「断面二次モーメント」があります。
断面二次極モーメント = 断面形状に対する断面二次モーメント + 90度回した断面形状に対する断面二次モーメント
となります。
断面が中実円の場合90度回しても断面二次モーメントはもちろん同じ。
なので中実円や中空円の場合次のように、断面二次モーメントから断面二次極モーメントを求めることができます。
極断面係数を計算する
極断面係数はその断面形状(寸法)がねじりに対してどれほど強いかを示す数値になります。
極断面係数は、断面二次極モーメントを半径で割ることで求めます。
極断面係数の式の分母のrをd/2(中実円), またはd_2/2(中空円)に置き換えて断面二次極モーメントの公式に置き換えれば以下となります。
つまり下の計算をすれば、断面二次極モーメントを計算するステップは省略出来るってことです。
せん断応力を計算する
これまでに計算したトルクと極断面係数より、ねじりによって発生するせんだん応力を求めます。
せん断応力を求める式はこちら。
ここで求めたせん断応力は軸の表面に発生する最大せん断応力です。
表面に発生するせん断応力が最大となり、中心に向かうに連れ応力は小さくなっていきます。
いくらねじっても中心のせん断応力は0(ゼロ)。
表面のせん断応力が降伏点に達しても中心部はまだ降伏していないことになりますが、表面のみでも降伏点を超えたら、機械部品としては「破損した」とみなしていいでしょう。
計算したせん断応力と材料のせん断強さを比較する
今までの計算でねじりによって発生するせん断応力が出ましたが、これをどう判断すればいいのでしょうか?
計算で求めたせん断応力は、極限せん断強さまたは降伏せん断強さと比較します。
- せん断応力 > 極限せん断強さ → ねじ切れる
- せん断応力 > 降伏せん断強さ → 力を取り除いても永久変形が残る
と考えられます。
じゃあ、極限せん断強さや降伏せん断強さの具体的な数字はいくらなの?と思いますが、この辺の数字は調べても出てこない場合が多いです。
JISでもSS400などの引張強さや引張の降伏点は定められていますが、せん断強さについては記載されていません。
ではどうするかというと、一般的に材料のせん断強さは引張強さの60%程度となり(軟鋼の場合)、これで強度計算します。
降伏せん断強さは、引張降伏強さの60%程度と考えます。
強度計算に使用するための、いくつかの金属材料の「引張強さ」と「せん断強さ」をまとめてみました。
引張強さの60%を極限せん断強さとしています。
※あくまで目安です。この数値が正しい保証はないのでしっかり調べてから設計してくださいね。
| 種類 | 記号 | 降伏点または耐力 N/mm2 (= MPa) | 引張強さ N/mm2 (= MPa) | 降伏せん断強さN/mm2 (= MPa) | 極限せん断強さN/mm2 (= MPa) |
|---|---|---|---|---|---|
| 一般構造用圧延鋼 | SS400 | 245 | 400~510 | 147 | 240~306 |
| 機械構造用炭素鋼 | S45C | 345 | 570 | 207 | 342 |
| 機械構造用合金鋼 | SCM435 | 785以上 | 930以上 | 471以上 | 558以上 |
| ステンレス | SUS304 | 205 | 520 | 123 | 312 |
| ステンレス | SUS430 | 205 | 420 | 123 | 252 |
| アルミ合金 | A5052(質別: O) | 65 | 170~215 | 39 | 102~129 |
| アルミ合金(超々ジュラルミン) | A7075(質別: T6) | 240~460 | 360~545 | 144~276 | 216~327 |
| タフピッチ銅 | C1100(質別: O) | 69以上 | 195以上 | 41.4以上 | 117以上 |
| 黄銅 | C2801 | – | 325~470以上 | – | 195~282以上 |
他に、機械設計製図便覧にも材料の強弱表としてせん断の極限強さの記載があるので抜粋して紹介します。
上の表よりはずっとあてになると思います。
| 材料 | 極限強さ・引張 N/mm2 (= MPa) | 極限強さ・せん断 N/mm2 (= MPa) |
|---|---|---|
| 錬鉄(繊維に平行) | 320~370 | 250~320 |
| 軟鋼 | 330~440 | 280~370 |
| 鋼 | 440~880 | >400 |
| 鋳鉄 | 120~235 | 130~250 |
| 鋳鋼 | 350 | 390 |
| 黄銅 | 150 | 150 |
または、JIS B8265「圧力容器の構造-一般事項 」の4.3.2項にこのような記述があります。
「設計温度における材料の許容せん断応力は許容引張応力の0.8倍とする。」
これに則れば0.8倍でもOKとなりますね。
より安全側で考えるなら0.6倍となりますが、どれを採用するかは設計者次第です。
安全率を考慮して許容応力を決める
SS400の極限せん断強さが240 MPaとして、設計した部品に発生するねじりによるせん断応力が230 MPaだったとします。
せん断強さ: 240 MPa > せん断応力: 230 MPa
せん断応力はせん断強さ以下だからOK!というわけにはいきません。
強度がギリギリの設計だと、ちょっとしたはずみで機械が壊れたり、材料内部の不均一、表面の傷の影響により計算よりも小さな荷重で壊れるかもしれません。
そこで極限強さに「安全率」を掛けて許容応力を決定します。
破壊する応力に対して、許容する応力の余裕を何倍とるか、ということです。
安全率の公式は以下です。
| S | 安全率 |
|---|---|
| σB | 極限強さ [MPa] |
| σa | 許容応力 [MPa] |
極限強さと安全率から許容応力を求めるように変形するとこうなります。
安全率を決めるため簡便に用いられているのが下表の「アンウィンの安全率」。
| 材料 | 固定荷重 | 繰返し荷重(片振り) | 交番荷重(両振り) | 衝撃荷重 |
|---|---|---|---|---|
| 鋳鉄 | 4 | 6 | 10 | 15 |
| 軟鋼 | 3 | 5 | 8 | 12 |
| 鋳鋼 | 3 | 5 | 8 | 15 |
| 銅および合金 | 5 | 6 | 9 | 15 |
| 木材 | 7 | 10 | 15 | 20 |
| 石材・コンクリート | 20 | 30 | (25) | (30) |
荷重の種類や材料によって安全率が変わってきます。
例えば材質がSS400の場合は上の表では「軟鋼」に該当し、固定荷重の場合は安全率が「3」となります。
先程の公式に当てはめると以下の計算により許容応力は80 MPaとなります。
部品に発生する応力が80 MPa以下になるように部品の断面積を調整するなど、設計に反映します。
- 極限強さ σB に「極限せん断強さ」を入れると破壊に対する安全率
- 極限強さ σB に「降伏せん断強さ」を入れると変形に対する安全率
となりますが、機械部品の軸は変形を許さない場合が多いと思いますので、そんなときは「降伏せん断強さ」を入れるとよいでしょう。
「SS400の許容応力は○○MPa」と言った一般的に決まった値はありません。
想定される荷重の種類、材質を考慮して設計者が許容応力を決めます。
仕様や社内の規格で決まっている場合はそちらに従いましょう。
許容応力のより詳しい求め方については下記記事で説明しています。
例題を計算してみる
ではいよいよ、例題を実際に計算していきましょう!
トルクの計算
まずこの状況で軸にどれだけのトルクがかかっているか計算します。
計算式に代入するパラメーターは図によると以下の値となります。
| r | 50 [mm] |
|---|---|
| W | 1000 [N] |
計算してみると、軸にかかるトルクは50,000 [N・mm]ということが分かりました。
極断面係数を計算
次に極断面係数を計算します。
今回は必要ないので、断面二次極モーメントの計算は省略して極断面係数を求めます。
この例では断面形状が中身の詰まった中実円なので、以下の公式を使います。
中空円の場合は式が変わりますので注意してください。
直径 dは10 mmなので、式に当てはめて計算すると、極断面係数は196.35 mm3となりました。
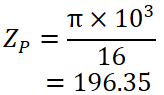
せん断応力を計算
いよいよせん断応力を計算します。
式に代入する値は先程計算した以下となります。
| T | 50000 [N・mm] |
|---|---|
| ZP | 196.35 [mm3] |
式に当てはめて計算すると、この軸がねじられて発生するせん断応力は254.65 MPaということが分かりました!
軸は壊れる?壊れない?
計算により、軸に発生するせん断応力は254.65 MPaと分かりましたが、この値をどう判断するか。
- せん断応力 > 極限せん断強さ → ねじ切れる
と考えることができ、SS400の極限せん断強さをここでは240 MPaとします。
ということは、
- せん断応力: 254.65 [MPa] > 極限せん断強さ: 240 [MPa]
となるため、残念ですがこの軸はねじれて破断する可能性があります。
軸の直径を大きくするなど、設計変更が必要ですね。
安全率を考慮して軸の直径を決定
この例題の軸の径はいくらにすれば良いのでしょうか?
SS400の極限せん断強さを240 [MPa]、
安全率を3に設定して許容応力を求めてみます。
以下の計算の通り、許容応力は80 MPaですね。

せん断応力を求めた式を逆算していって80 MPaになる直径を計算することも出来ますが、面倒くさいですよね。
実務的にはExcelで計算書を作っておくと、直径を変えた時に応力がいくらになるか瞬時に計算出来るので便利です。
Excelにグラフを描かせると直径とせん断応力の関係を視覚的に判断できます。
今回の例題でのグラフが上ですが、せん断応力が80 MPaになるのは軸の直径が15 mmくらいのときですね。
軸径15 mmで改めて計算してみると、せん断応力は75.45 MPaでした。
許容応力の80 MPa以下となったので、OKです!
他にもグラフを見れば、「直径30mm以上になると応力は横ばいになるので、それ以上増やしてもあんまり意味ないな」みたいな判断もできます。
まとめ
ねじり応力の計算は次のステップで出来ます。
- ねじりモーメント(トルク)を計算する
- 断面二次極モーメントを計算する(省略可能)
- 極断面係数を計算する
- ねじりの公式でせん断応力を計算する
今回は発生する応力を基準に軸サイズを決める方法を紹介しましたが、変形量(ねじれた角度)を基準に軸の直径を決める方法もあります。
ねじり以外の強度計算は下記の記事が参考になります。




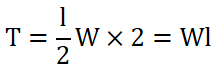

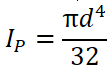


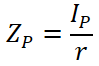
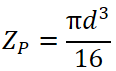



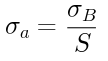
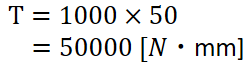
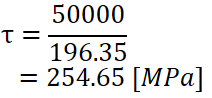



コメント