ある部品を引っ張ったり、他の部品を吊るしたとき、どれほどの荷重(力)で破壊されるのか、と言った機械設計における強度計算方法を説明します。
引張以外の強度計算については下記記事が参考になります。
引張荷重を加えた部品が何mm変形(伸び)するかのの計算は下記の記事が参考になります。
この記事の目次
この設計で壊れる?壊れない?
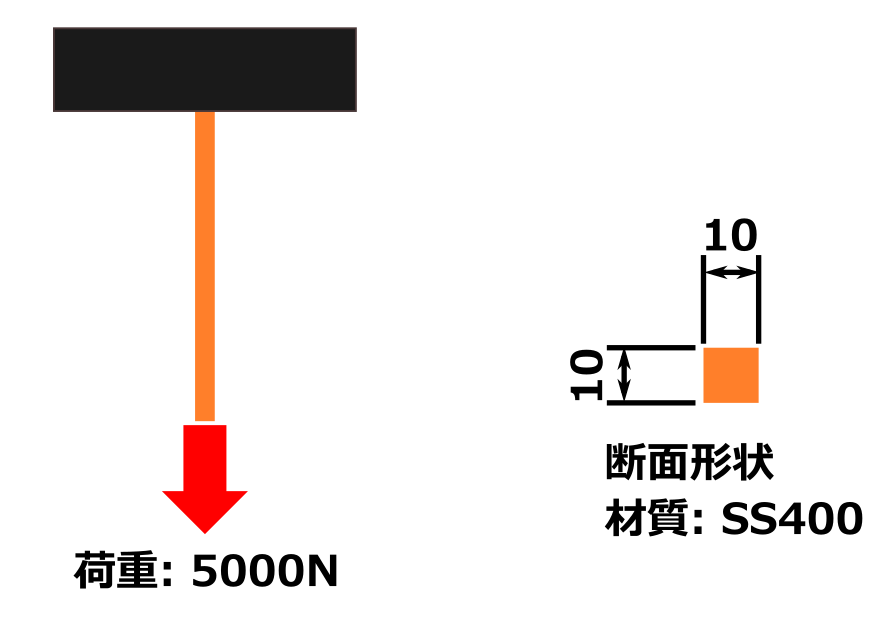
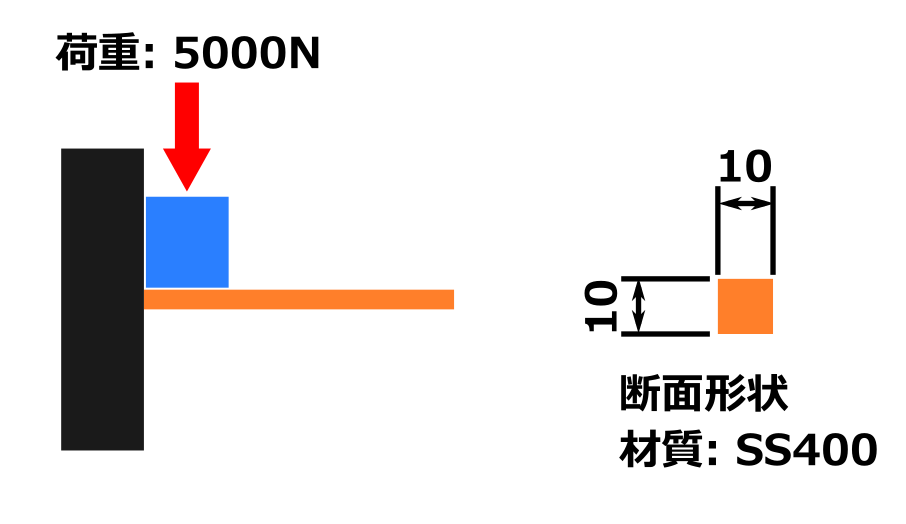
この図のような状況のとき、このオレンジ色の棒状の部品が壊れるのか、壊れないのか?またどの程度の力を加えるとちぎれて破壊(破断)するのかということを求めていきます。
- 部品の断面は 10 mm × 10 mmの正方形
- 材質:SS400
- 5000Nの引張荷重がかかる
という条件です。
※ 棒の自重は無視して計算します。
引張強度の計算の概要
今回の強度計算は次の2ステップで求められます。
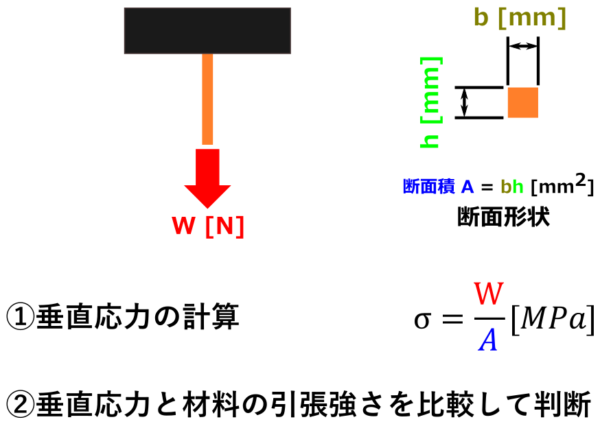
- 強度計算したい部品の断面積と荷重より垂直応力を求める
- 垂直応力が材料の引張強さより大きければ壊れる、小さければ壊れないと判断する
単純に壊れる、壊れないではなく、永久ひずみが残っては困る場合には、引張強さではなく降伏点と垂直応力を比較します。
垂直応力の計算方法
まず、材料を引っ張った時に、材料内部に発生する「応力」を計算します。
応力とは、引っ張られた材料がちぎれまいと踏ん張る力、と言ったところですかね。
応力にもいくつか種類がありますが、今回の例のように引っ張ったり、圧縮したりする場合の応力を「垂直応力」と呼び記号σ(シグマ)で表します。
垂直応力の公式はこうです。
図より、荷重は5000 Nですが断面積が不明なので計算します。
1辺10mmの正方形なので、以下の通り断面積は100 mm^2です。
10 × 10 = 100 [mm2]
先程の公式に当てはめると以下の計算の通り50 MPaとなります。
[mntyzer_topmedium]
求めた応力を材料の引張強さや降伏点と比較する
材料ごとに引張等に耐えられる応力が決まっていて、その応力を超えたとき、材料は破断したり永久に変形したりします。
今回の例の材質はSS400と言う軟鋼。
その名の通り400 MPaの引張強さとなっています。(実際はちょっと違いますが、ここでは400 MPaとして計算します)
先程の計算で部品に発生する垂直応力が50 MPaなので、
引張強さ 400 [MPa] > 垂直応力 50 [MPa]
となり、全然余裕で部品は破壊しないことが分かります。
ちなみに何Nの荷重でこの部品がちぎれて壊れるかと言うと、荷重Wを求める形に公式を変形して
W = σA
数値を代入して計算すると
W [N] = 400 [MPa] × 100 [mm2]
= 40000 [N]
となり、40000 N (40 kN)で破断することになります。
ざっくり4 tくらいの物体を吊り下げられることになりますね。
応力と力(荷重)は何が違う?
先程の強度計算では「垂直応力」を求めて、材料の引張強さなどと比較しました。
なぜ応力を求める必要があるのでしょうか?
応力を求める公式は以下の通り、荷重を断面積で割っています。
つまり断面積が大きいほど内部に発生する応力が小さくなる = 部品が壊れにくくなるわけです。
サイズの違う部品Aと部品Bがあったとして、同じく5000 Nの荷重がかかっているとします。
部品Aの断面積は100 mm2、部品Bの断面積は1 mm2です。
部品Aに発生する応力は50 MPa。
σ = 5000 / 100
= 50 [MPa]
一方部品Bに発生する応力は5000 MPa。
σ = 5000 / 1
= 5000 [MPa]
材質がSS400として、引張強さが400 MPaなので、部品Bはいとも簡単にちぎれてしまうことが分かります。
このように、同じ5000 Nでも断面積が異なると結果が全然違ってくるので、強度計算の際には応力で考えるわけです。
材料の「引張強さ」と「降伏点」とは?
材料の強度計算をする上で重要な数値に「引張強さ」と「降伏点」があります。
これらは材料ごとに決まっている数値で、以下のような値となります。
| 種類 | 記号 | 降伏点または耐力 N/mm2 (= MPa) | 引張強さ N/mm2 (= MPa) |
|---|---|---|---|
| 一般構造用圧延鋼 | SS400 | 245 | 400~510 |
| 機械構造用炭素鋼 | S45C | 345 | 570 |
| ステンレス | SUS304 | 205 | 520 |
| ステンレス | SUS430 | 205 | 420 |
| アルミ合金 | A5052(質別: O) | 65 | 170~215 |
| 超々ジュラルミン | A7075(質別: T6) | 240~460 | 360~545 |
| ねずみ鋳鉄 | FC200 | – | 200以上 |
| タフピッチ銅 | C1100(質別: O) | 69以上 | 195以上 |
| 黄銅 | C2801 | – | 325~470以上 |
| 樹脂 | ABS | – | 61 |
| 樹脂 | PP | – | 35 |
| 樹脂 | PE | – | 24 |
| 樹脂 | PMMA | – | 67 |
| 樹脂 | PC | – | 61 |
| 樹脂 | PA66 | – | 82 |
※あくまで参考値です。実際に設計する際はJIS規格、樹脂メーカーのデータシート等でしっかり確認してください。
熱処理の仕方や、樹脂のグレードや温度によって値はいくらでも変わってきます。
引張強さとは、それ以上の応力が発生すると材料がちぎれたりして破壊する限界の強さを表します。
降伏点とは、それ以上の応力が発生すると、力を取り除いても部品に永久ひずみが残る強さです。
つまり、部品が伸びたり曲がったりして元に戻らないことを意味します。
降伏点以下の力であれば、力を加えている最中は多少の変形はすれど、力を取り除くと元の寸法に戻ります。
これを「弾性変形」と言います。
「とにかく部品が破壊しなければ良い(変形してもいい)」という場合は「引張強さ」を基準に設計し、
「永久的な変形は許されない」という場合は「降伏点」を基準に設計します。
大抵の機械は部品が変形したら困るので、降伏点を基準に設計することが多いかと思います。
上の表では「降伏点または耐力」となっていますが、アルミ合金などは材料を試験しても降伏点がはっきり現れないため、永久ひずみが0.2%となるときの応力を降伏点の代わりに設計に用います。
- 軟鋼の応力ひずみ線図の例
- アルミの応力ひずみ線図の例
引張強さや降伏点に安全率を掛けて許容応力を決める
SS400の引張強さが400 MPaとして、設計した部品に発生する応力が390 MPaだったとします。
400 MPa > 390 MPa
応力は引張強さ以下だからOK!というわけにはいきません。
強度がギリギリの設計だと、想定外の外力が少し加えられただけでも壊れる可能性があります。
そこで登場するのが「安全率」という考え方。
破壊する応力に対して、許容する応力の余裕を何倍とるか、ということです。
安全率の公式は以下です。
極限強さと安全率から許容応力を求めるように変形するとこうなります。
安全率をいくらにするか、というのも諸説ありますが、簡便に用いられているのが下表の「アンウィンの安全率」。
| 材料 | 固定荷重 | 繰返し荷重(片振り) | 交番荷重(両振り) | 衝撃荷重 |
|---|---|---|---|---|
| 鋳鉄 | 4 | 6 | 10 | 15 |
| 軟鋼 | 3 | 5 | 8 | 12 |
| 鋳鋼 | 3 | 5 | 8 | 15 |
| 銅および合金 | 5 | 6 | 9 | 15 |
| 木材 | 7 | 10 | 15 | 20 |
| 石材・コンクリート | 20 | 30 | (25) | (30) |
荷重の種類や材料によって安全率が変わってきます。
例えば材質がSS400の場合は上の表では「軟鋼」となり、固定荷重の場合は安全率が「3」となります。
先程の公式に当てはめると以下の計算により許容応力は133.3 MPaとなります。
部品に発生する応力が133.3 MPa以下になるように部品の断面積を調整するなど、設計に反映します。
極限強さを何に設定するかですが、材料が破壊するかどうかを基準にする場合は引張強さに、材料が永久変形するかどうかを基準にする場合は降伏強さを設定すると良いでしょう。
「SS400の許容応力は○○MPa」と言った一般的に決まった値はありません。
どのような種類の荷重が加わるかを見極めて安全率を設定することから、許容応力はあくまで設計者が決める数値となります。
または仕様で決まっている場合もあります。
許容応力のより詳しい求め方については下記記事で説明しています。
引っ張り応力と圧縮応力
軟鋼の場合、引張と圧縮の許容応力は同等と見積もってよいですが、部品が長い場合は圧縮強度より座屈強度が重要になってきます。
細長い針金に両側から力を加えると、圧縮で破壊される前に、くにゃっと座屈して曲がってしまうのがイメージできるかと思います。
座屈については下記の記事で計算方法を説明していますが、細長い部品に圧縮荷重を加えるときは注意が必要です。
まとめ
部品が引張に耐えられるかどうかの強度計算は次の2ステップで求められます。
- 強度計算したい部品の断面積と荷重より垂直応力を求める
- 垂直応力が材料の引張強さより大きければ壊れる、小さければ壊れないと判断する
引張以外の強度計算については下記記事が参考になります。

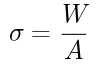
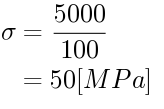



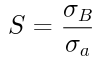



コメント