機械設計において、はりのたわみ(変形量)を計算する機会は数多くあります。
今回は比較的単純な荷重条件のたわみの計算方法を説明します。
荷重を加えたはりが曲げ応力やせん断応力により破壊するかの計算は下記が参考になります。
この記事の目次
はりのたわみとは?
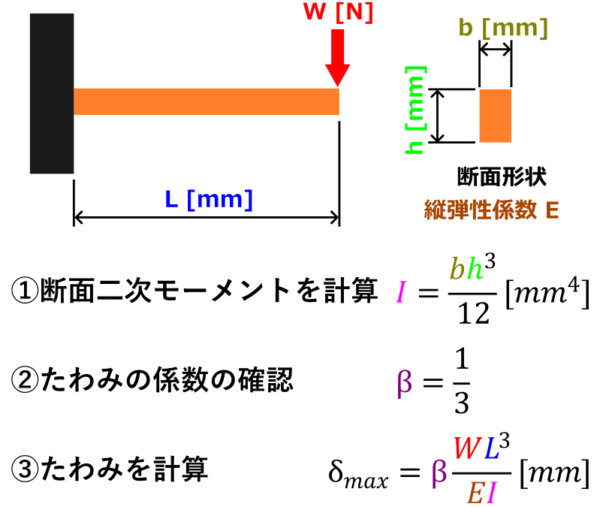
そもそも「はりのたわみ」というのは、下の図のように部材に力を加えるとしなるように曲がることです。
力を取り除くと元の形に戻ります。
「はり」と言うと、家やビルの構造材を想像してしまいますが、鉛筆でもメガネのツルでも、多くのものは「はり」と見なして強度や変形量を計算することが出来ます。
例えば鉄棒にぶら下がった時、実感としてはあまり分からないですが、鉄の棒が体重でたわんでいます。
他の例ではプラスチックの定規の片端を持ってもう一方に力を加えるとたわみますよね。
材料力学の知識があればこの変形量を計算することが出来ます。
はりのたわみ計算の例題
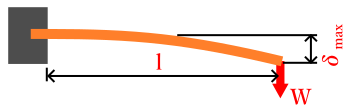
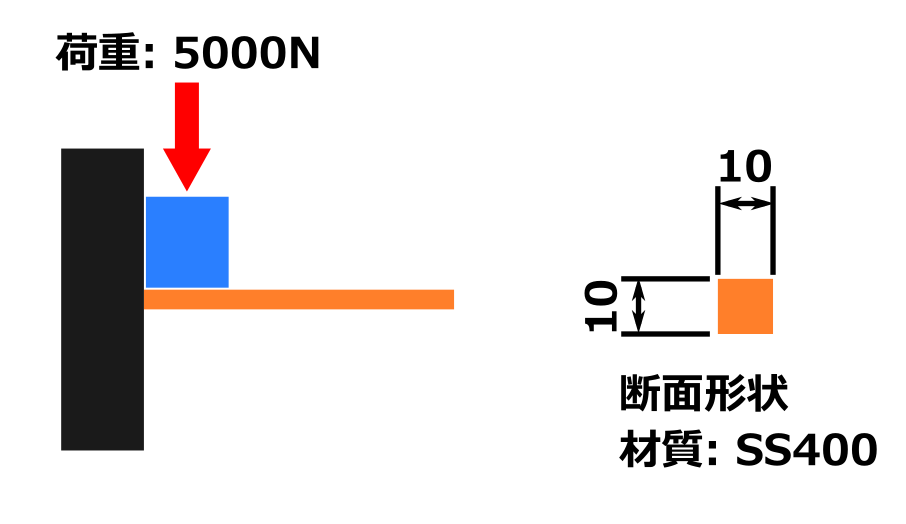
下の図のような状況の時の、はりの最大たわみはいくらになるでしょうか?

下記の条件で、先端の最大たわみが何mmになるかを計算したいと思います。
- はりの種類と荷重条件: 片持集中荷重
- 荷重 1,000 N
- はりの長さ(スパン): 300 mm
- はりの断面: 高さ 30 mm、幅 10 mm
- 材質(縦弾性係数): SS400 (206,000 MPa)
もちろんですが、はりの先端で最大たわみとなります。
[mntyzer_topmedium]
計算方法概要
はりのたわみは次のステップで計算出来ます。
- 断面二次モーメントを計算
- たわみの係数の確認
- たわみを計算
今回は下記のような条件の、シンプルな荷重の加わり方についての説明となります。
- 片持ばりの場合ははりの先端に荷重を加える
- 両端支持や両端固定の場合ははりの中央に荷重を加える
- 等分布荷重の場合は全長にわたり均等に荷重を加える
計算方法詳細
それでは、はりのたわみの計算方法を見ていきましょう。
計算方法の詳細説明 → 例題を計算という流れで説明します。
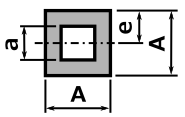
断面二次モーメント計算
まず断面二次モーメントの計算をします。
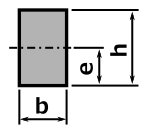
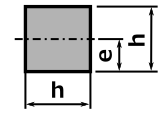
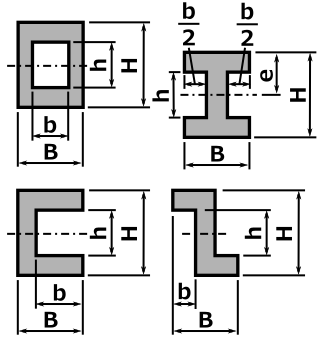
断面形状により計算方法が変わってくるので、下の表より断面形状を選んで計算してください。
|
断面 |
断面積 A |
重心の距離 e |
断面二次モーメント I |
断面係数 Z = I / e |
 |
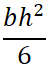 |
|||
 |
||||
 |
 |
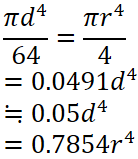 |
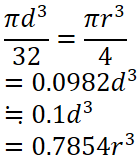 |
|
 |
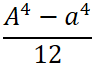 |
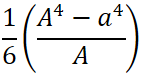 |
||
 |
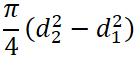 |
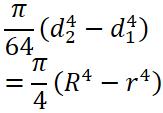 |
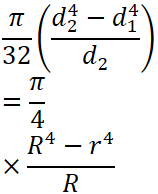 |
|
 |
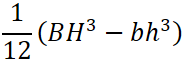 |
 |
例題の計算
例題では長方形断面なので断面二次モーメントを求めるのは次の式になります。
長方形断面の断面二次モーメントの式
\[ I=\frac{bh^3}{12}[mm^4] \]
| I | 最小断面二次モーメント [mm4] |
|---|---|
| b | 断面の幅 [mm] |
| h | 断面の高さ [mm] |
例題のはりの断面形状より、b, hの値は下記となります。
| b | 20 [mm] |
|---|---|
| h | 30 [mm] |
式に代入して計算すると、断面二次モーメントは45,000 mm4となりました。
\[\begin{eqnarray}
I&=&\frac{20\times{30}^3}{12}\\
&=&45000[mm^4]
\end{eqnarray}\]
等分布荷重はトータルの荷重で考える
材料力学の問題では等分布荷重の条件が「100 N/mm」みたいに示されていることが多いです。
この等分布荷重が500 mmに渡って加わっているとしたら、次の計算の通り合計で50,000 Nの荷重がかかっているとして計算します。
\[\begin{eqnarray} W&=&wl\\
&=&100\times500\\
&=&50000\ [N]
\end{eqnarray}\]
ただ実際の設計では「100 N/mm」みたいに荷重の状態が示されていることは、あまりないと思いますが…
はり自体の自重によるたわみを計算する場合は、等分布荷重と見なせます。
はりの重量がわかっている場合は、
- はりの質量 m kg
- 重力加速度 9.8 m/s2
として、運動方程式 F = ma [N] より、
9.8m [N]の荷重と考えればOKです。
たわみの係数の確認
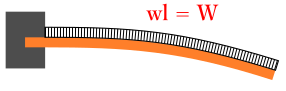
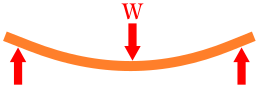
はりの種類と荷重の加わり方により「たわみの係数」を選択します。
はりの種類は「片持」、「両端支持」、「両端固定」等があり、荷重の加わり方は「集中荷重」と「等分布荷重」があります。
「片端支持、片端固定」や先端以外や中央以外への荷重等のややこしいことは今回は考えません。
次の表にて、はりの種類と荷重の加わり方によるたわみの係数を選択してください。
| はりの種類 | たわみの係数 β | δmaxの位置 |
|---|---|---|
 |
1/3 | 自由端 |
 |
1/8 | 自由端 |
 |
1/48 | 中央 |
 |
5/384 | 中央 |
 |
1/192 | 中央 |
 |
1/384 | 中央 |
例題の計算
例題は片持ばりで集中荷重なので、たわみの係数は1/3です。
この係数はたわみの計算の時に使います。
縦弾性係数の確認
計算するたわみは弾性変形のため、はりの材料の縦弾性係数の値が必要になります。
参考までに主な材質の縦弾性係数一覧を載せておきます。
値の正確さは保証できませんので、必要に応じて各自JISや資料等で調べてくださいね。
(材料力学の参考書にはなぜかあんまり載ってないです。)
※樹脂材料の縦弾性係数は引張弾性率を記載
| 材質 | 縦弾性係数 E [MPa (N/mm2)] |
|---|---|
| 軟鋼(SS400) | 206,000 |
| 鋼(SCM435) | 214,000 |
| ステンレス(SUS304) | 193,000 |
| リン青銅(C5191) | 105,000 |
| アルミニウム(A5052) | 72,000 |
| 銅(C1100) | 118,000 |
| 樹脂(ABS) | 3,050 |
| 樹脂(PP) | 1,500 |
| 樹脂(PE) | 1,000 |
| 樹脂(PMMA) | 3,300 |
| 樹脂(POM) | 2,350 |
| 樹脂(PC) | 2,400 |
| 樹脂(PA66) | 3,000 |
資料によっては単位が GPaのことが多いですが、ここでは MPaにしています。
GPaのまま計算すると結果が3桁変わってくるので注意してください。
例題の計算
例題の画像には縦弾性係数がすでに書かれていますが、材質は軟鋼のSS400なので、縦弾性係数は206,000 MPaとなります。
たわみの計算
断面二次モーメントやたわみの係数など、計算に必要なパラメータが揃ったので、いよいよ大詰めです。
あとはたわみの式に代入して計算するだけ。
\[ \delta_{max}=\beta\frac{WL^3}{EI} \]
| δmax (デルタ) | 最大たわみ [mm] |
|---|---|
| β (ベータ) | たわみの係数 |
| W | 荷重 [N] |
| L | はりの長さ(スパン) [mm] |
| E | 縦弾性係数 [MPa] |
| I | 最小断面二次モーメント [mm4] |
例題の計算
では例題の方を計算してみましょう。
たわみを求める式に代入するパラメータは下記になります。
| β (ベータ) | 1/3 |
|---|---|
| W | 1000 [N] |
| L | 300 [mm] |
| E | 206000 [MPa] |
| I | 45000 [mm4] |
計算してみると、たわみは0.97mmになりました!
\[\begin{eqnarray} \delta_{max}&=&\frac{1}{3}\times\frac{1000\times{300}^3}{206000\times45000}\\ &=&0.97\ [mm] \end{eqnarray}\]
たわみ角の計算(必要な場合のみ)
必要であればたわみ角の計算をします。
例えば、片持はりの先端に光電センサがついていて、はりのたわみにより光軸の方向がどう変化するか?みたいな状況です。
今回は片持はりのたわみ角の計算方法を紹介します。
片持はりのたわみ角の式
\[ i_{max}=\frac{WL^2}{2EI}[rad] \]
| imax | 最大たわみ角 [rad] |
|---|---|
| W | 荷重 [N] |
| L | はりの長さ(スパン) [mm] |
| E | 縦弾性係数 [MPa] |
| I | 最小断面二次モーメント [mm4] |
片持はりや両端支持ばりの任意の位置のたわみ角やたわみ量の計算方法は、下記の書籍に掲載されています。
興味があればご確認ください。
例題の計算
例題の最大たわみ角を計算してみます。
| W | 1000 [N] |
|---|---|
| L | 300 [mm] |
| E | 206000 [MPa] |
| I | 45000 [mm4] |
式に代入して最大たわみ角を計算すると、0.00495 radになりました。
\[\begin{eqnarray} i_{max}&=&\frac{1000\times300L^2}{2\times206000\times45000}\\ &=&0.00495[rad] \end{eqnarray}\]
度に換算すると0.28 度になります。
たわみと同時に曲げ応力も必ず確認すること
たわみ量の計算式の中で縦弾性係数を使っていることから分かるように、この計算は材料の比例限度内でのみ成り立ちます。
材料の比例限度が分からないことも多いため、ざっくり降伏点以下で成り立つと考えて大きな問題は無いでしょう。(降伏点は調べたら分かることが多いです)
そのため、荷重を加えた時の部材内に発生する応力が、材料の降伏点を超えていないかの確認も必ずしましょう。
たわみの計算をしても、降伏点を超えている場合は全く意味のないものになってしまいます。
曲げ応力の計算方法は下記の記事が参考になります。
例題の計算
では今回の例題では曲げ応力はいくらになるのか?
計算の過程は省きますが、答えはちょうど100 MPaとなります。
SS400の降伏点が245 MPaとして、十分余裕があるのでたわみ量が0.97 mmと言う計算結果はある程度妥当と考えられます。
仮に曲げ応力が降伏点を超えてしまっていた場合、降伏点以降はひずみが急激に大きくなるため、計算結果の0.97 mmよりも変形量が大きくなる可能性が高いです。
実際はせん断による滑り変形も発生するが無視する
今回の例のように荷重を加えると、曲げによるたわみの他に、せん断による滑り変形も同時に発生します。
しかし、せん断による滑り変形量は非常に小さいため、無視しても実用上は問題ありません。
せん断による滑り変形の計算は下記の記事が参考になります。
実際に計算してみると、せん断による滑り変形の小ささが実感できます。
まとめ
はりのたわみは次のステップで計算出来ます。
- 断面二次モーメントを計算
- たわみの係数の確認
- たわみを計算



コメント