ねじりを受ける機械部品は丸棒やパイプ等、円形断面の軸が多いですが、長方形や四角形等、矩形の断面形状部材にねじり応力(せん断応力)が発生することもあります。
そんな長方形、正方形部材がねじられたときに発生する応力の計算方法について説明します。
この記事を読めば、矩形の構造材のねじりの強度計算が出来るようになります。
円形断面(中実円、中空円)の軸のねじりについてはこちらの記事で説明しています。
ねじり以外の強度計算は下記の記事が参考になります。
この記事の目次
例題
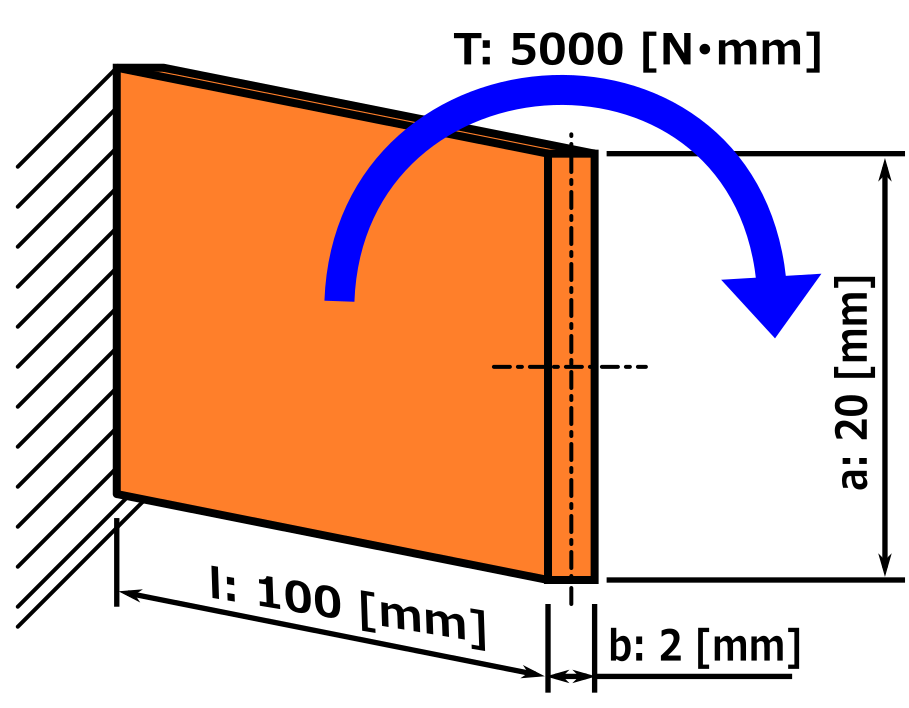
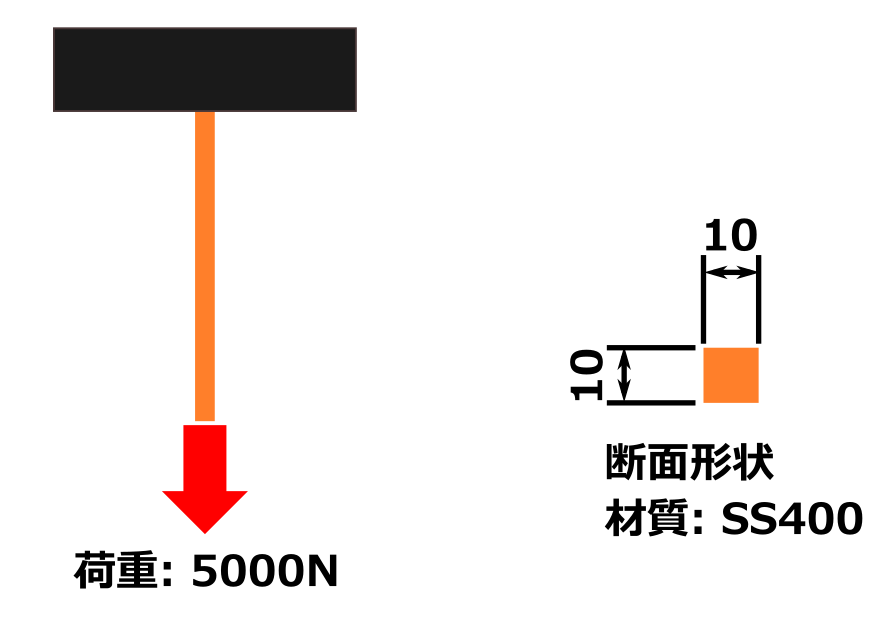
例題として下の画像のような長方形断面の軸と言うか構造材のねじりを、実際に計算してみます。
はたしてこの部材は壊れるのか、壊れないのか?

条件
- 断面形状: 幅2 mm、高さ20 mm
- 長さ100 mm
- 5000 N・mm(= 5 N・m)のトルクがかかっている
- 材質 SS400
まずは長方形断面のねじりの計算方法を説明して、その後この例題の強度を計算してみます。
長方形断面のねじりの計算の概要
長方形断面のねじり応力、ねじれ角は次のステップで計算出来ます。
- 長辺と短辺の長さの比より係数を確認
- 発生するせん断応力(ねじり応力)を計算
- 比ねじれ角を計算
- ねじれ角を計算

| a | 長辺の長さ [mm] |
|---|---|
| b | 短辺の長さ [mm] |
| τ1 | 最大せん断応力 [MPa] |
| k1 | 係数 |
| k3 | 係数 |
| θ (シータ) | 比ねじれ角 [rad/mm] |
| Φ (ファイ) | ねじれ角 [rad] |
円形断面のときと計算の手順がだいぶ違いますね。
円形断面では極断面係数を計算しましたが、長方形断面では計算しません。
部材をねじるとせん断応力が発生しますが、ねじったときに発生するせん断応力を「ねじり応力」とも呼びます。
長方形断面のねじりの計算方法
長方形断面のねじりの計算方法の詳細について説明していきます。
長辺と短辺の長さの比より係数を確認
まず長辺、短辺の比より係数を確認します。
a ÷ bした値と、表の「a/b」の値が近いところの係数 K1~K3を計算に使用します。
係数の表
| a/b | 1.0 | 1.25 | 1.5 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 8.0 | 10.0 | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | 0.208 | 0.221 | 0.231 | 0.246 | 0.267 | 0.282 | 0.29 | 0.299 | 0.307 | 0.312 | 0.333 |
| K2 | 1 | 0.916 | 0.859 | 0.795 | 0.753 | 0.745 | 0.744 | 0.743 | 0.742 | 0.742 | 0.742 |
| K3 | 0.141 | 0.172 | 0.196 | 0.229 | 0.263 | 0.281 | 0.29 | 0.299 | 0.307 | 0.312 | 0.333 |
例えば長辺が14mm短辺が5mm、だったら、14 / 5 = 2.8。
表の「a/b」では3.0が近いので以下の値を用いる感じです。
- K1 = 0.267
- K2 = 0.753
- K3 = 0.263
長方形断面のねじり応力の式
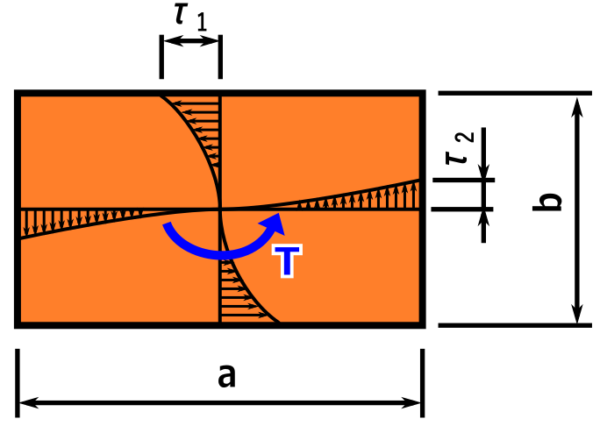
長方形のねじり応力(せん断応力)は長辺側と短辺側で異なります。
それぞれを求める式は以下です。
![τ_1=τ_max=T/(K_1 ab^2 ) [MPa]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_04.png)
![τ_2=K_2 τ_1 [MPa]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_05.png)
| τ1 | 最大せん断応力(長辺中央) [MPa] |
|---|---|
| τ2 | せん断応力(短辺中央) [MPa] |
| T | ねじりモーメント(トルク) [N・mm] |
| k1 | 係数 |
| k2 | 係数 |
| a | 長辺の長さ [mm] |
| b | 短辺の長さ [mm] |
比ねじれ角の計算
比ねじれ角とは、単位長さあたりのねじれ角です。
ねじれの度合いを表します。
比ねじれ角の式
$$\LARGE
\theta=\frac{T}{K_3ab^3G}[rad/mm]
$$
| θ (シータ) | 比ねじれ角 [rad/mm] |
|---|---|
| T | ねじりモーメント(トルク) [N・mm] |
| k3 | 係数 |
| a | 長辺の長さ [mm] |
| b | 短辺の長さ [mm] |
| G | 横弾性係数 [MPa] |
横弾性係数 Gは材料によって決まっている値で、せん断変形のしやすさを表します。
参考に主な材料の横断線係数を下記に示します。
<参考>主な材料の横弾性係数
| 材料 | 横弾性係数(MPa) |
|---|---|
| 錬鉄 | 75,000 |
| 軟鋼 | 79,000 |
| 鋼 | 83,000 |
| ばね鋼(焼入れなし) | 83,000 |
| ばね鋼(焼入れ) | 83,000 |
| 鋳鉄 | 26,000~39,000 |
| 鋳鋼 | 81,000 |
| 黄銅(鋳) | 29,000 |
| 黄銅(圧延) | 49,000 |
| アルミニウム | 25,000 |
| 銅 | 39,000 |
ねじれ角の計算
比ねじれ角は単位長さあたりのねじれ角でしたが、全体でいくらねじられたかが「ねじれ角」です。
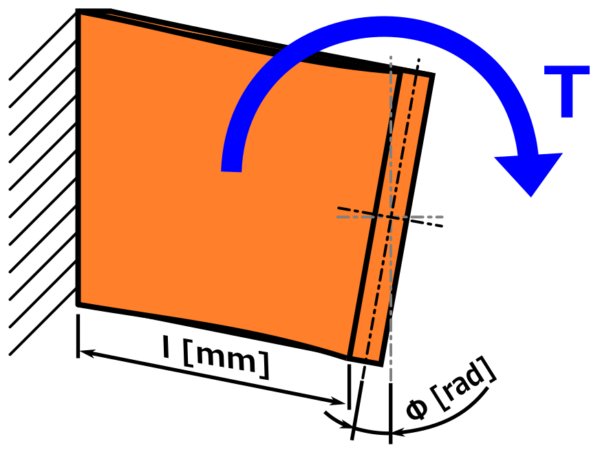
ねじれ角は次の計算で求められます。
ここで求めたねじれ角の単位は「ラジアン」となります。
必要があれば直感的に分かりやすい「°(度)」に換算しましょう。
せん断応力(ねじり応力)の判定
計算した応力で軸が破壊したり永久変形したりするか、詳しくは以下の記事で説明しています。
【材料力学】ねじり応力の計算方法・軸が破壊するトルクと寸法の決め方|丸棒,パイプの場合
ざっくり説明すると、計算したせん断応力(ねじり応力)が、材料の引張強さ×0.6を超えると破断、引張の降伏点(耐力)×0.6を超えると永久変形が発生すると考えられます。
例題を実際に計算してみる
それでは例題を実際に計算してみましょう。

長辺と短辺の長さの比より係数を確認
まず長辺、短辺の比より係数を確認します。
長辺 a: 20 mm、短辺b: 2 mmなので、a/b = 20/2 = 10
下の表で「a/b」が10のとこを見ると、係数は以下の値となります。
- K1 = 0.312
- K2 = 0.742
- K3 = 0.312
係数の表
| a/b | 1.0 | 1.25 | 1.5 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 8.0 | 10.0 | ∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | 0.208 | 0.221 | 0.231 | 0.246 | 0.267 | 0.282 | 0.29 | 0.299 | 0.307 | 0.312 | 0.333 |
| K2 | 1 | 0.916 | 0.859 | 0.795 | 0.753 | 0.745 | 0.744 | 0.743 | 0.742 | 0.742 | 0.742 |
| K3 | 0.141 | 0.172 | 0.196 | 0.229 | 0.263 | 0.281 | 0.29 | 0.299 | 0.307 | 0.312 | 0.333 |
長方形断面のねじり応力の式
係数が決まったので、ねじり応力を計算します。

![τ_1=τ_max=T/(K_1 ab^2 ) [MPa]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_04.png)
![τ_2=K_2 τ_1 [MPa]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_05.png)
| τ1 | 最大せん断応力(長辺中央) [MPa] |
|---|---|
| τ2 | せん断応力(短辺中央) [MPa] |
| T | ねじりモーメント(トルク) [N・mm] |
| k1 | 係数 |
| k2 | 係数 |
| a | 長辺の長さ [mm] |
| b | 短辺の長さ [mm] |
上の式に次のパラメータを代入して計算します。
| T | 5000 [N・mm] |
|---|---|
| k1 | 0.312 |
| k2 | 0.742 |
| a | 20 [mm] |
| b | 2 [mm] |
![τ_1=5000/(0.312×20×2^2 ) =200.3 [MPa]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_10.png)
![τ_2=0.742×200.3 =148.6 [MPa]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_11.png)
上記計算により、長辺の中央に発生する最大せん断応力は200.3 MPa、短辺中央のせん断応力は148.6 MPaということが分かりました。
最大せん断応力は長辺側中央のτ1となるので、特に必要なければτ2は計算しなくてもOKです。
比ねじれ角の計算
次に比ねじれ角の計算。
最大せん断応力さえ分かれば良い場合は計算しなくても大丈夫です。
比ねじれ角の式
$$\LARGE
\theta=\frac{T}{K_3ab^3G}[rad/mm]
$$
| θ (シータ) | 比ねじれ角 [rad/mm] |
|---|---|
| T | ねじりモーメント(トルク) {N・mm] |
| k3 | 係数 |
| a | 長辺の長さ [mm] |
| b | 短辺の長さ [mm] |
| G | 横弾性係数 [MPa] |
今回の例では、代入していくパラメータは次になります。
| T | 5000 [N・mm] |
|---|---|
| k3 | 0.312 |
| a | 20 [mm] |
| b | 2 [mm] |
| G | 79000 [MPa] |
$$\large\begin{eqnarray}
\theta&=&\frac{5000}{0.312\times20\times2^3\times79000} \\
\\
&=&0.001268[rad/mm]
\end{eqnarray}$$
式に当てはめて計算すると比ねじれ角は0.001268 rad/mmとなりました。
ねじれ角の計算
比ねじれ角は単位長さあたりのねじれ角なので、そのままでは軸端でどれだけねじれるか分かりません。
最終的にこの軸がどれほどねじれるかをあらわす「ねじれ角」を計算します。
次の値を式に代入して計算します。
| θ (シータ) | 0.001268 [rad/mm] |
|---|---|
| l | 100 [mm] |
![Φ=0.001268"×100" "=0.1268 [rad]"](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_13.png)
ねじれ角は0.1268 radということが分かりました。
単位がラジアンだと分かりにくいので度に換算してみます。
![0.1268×180/π=7.264 [°]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_14.png)
ねじれ角は7.264 °となりました。
でもちょっと待ってください。
このねじれ角を簡単に信用しちゃいけませんよ!
発生するせん断応力がせん断降伏強さを超えてないか確認が必要です。
計算した応力が降伏せん断強さを超えてないか確認する
降伏せん断強さを引張降伏断強さ×0.6と考える場合、
引張降伏断強さ 235 ×0.6 = 降伏せん断強さ 141.0 [MPa]
となります。(SS400の場合)
計算したねじり応力は200.32 MPaですので、降伏せん断強さを超えています。
応力とひずみが比例するのを「フックの法則」といいますが、これが成り立つのは比例限度以下です。
応力ひずみ線図を思い出してみると、降伏点を超えると応力を増やさなくてもひずみが増大します。
つまり計算結果よりもさらにねじれる可能性が高く、今回の例題で計算したねじれ角度はあまり意味をなさないことになります。
計算したねじれ角は、材料の比例限度以下の応力のときにのみ成り立ちます。
現実は材料の比例限度がいくらか?というデータはあまり出回ってないので、発生応力が降伏せん断強さ以下の場合に成り立つと考えとけば、機械設計の実務的には問題ないでしょう。
円形の断面以外をねじると断面が反る
円形の断面の軸をねじっても断面は平面のままです。
しかし円形以外の断面、例えば長方形断面はねじると長方形が平面じゃなくなり反ります。
この断面の反りを拘束するとねじれ角が小さくなります。
例題の図はよく見ると、長方形断面の軸が壁に固定されていますね。
つまり片側の断面が反らないように拘束されていると考えれば、計算結果よりもねじれ角は小さい、ということになりますね。
この辺は材料力学よりも、弾性力学が扱う分野となるようです。
最大応力は長辺の中央に発生する
計算式を見てたらお気づきかもしれませんが、長方形断面の軸をねじったときに発生する最大の応力は長辺中央のτ1に現れます。
円形断面の最大応力は中心から一番遠い外周部に現れます。
なので、なんとなく中心から一番遠いところ、つまりτ2に最大応力が発生するような気がしますよね?
でも実際は長辺中央のτ1に最大応力が現れますので、注意しましょう。

長方形断面のねじりの式が載っている書籍紹介
今回紹介した長方形断面のねじりの式はこちらの書籍に掲載されています。
わかりやすい材料力学の基礎 第2版
まとめ
長方形断面のねじり応力、ねじれ角は次のステップで計算出来ます。
- 長辺と短辺の長さの比より係数を確認
- 発生するせん断応力を計算
- 比ねじれ角を計算
- ねじれ角を計算
ねじれ角を見るときはせん断応力が降伏せん断強さを超えてないか確認を。
ねじり以外の強度計算は下記の記事が参考になります。
![Φ=θl[rad]](https://kawahara-zakki.com/wp-content/uploads/2022/10/rectangle-torsional-stress_08.png)
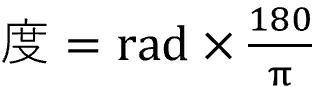


コメント
コメントで指摘頂いた単位の誤記について記事を修正しました。
コメントありがとうございます。
本当ですね。
おっしゃる通り、この記事では単位長さがmmなので、比ねじれ角の単位は[rad/mm]ですね。
記事の内容は時間のあるときに修正しておきます。
ご指摘ありがとうございます。
大変勉強になりました。比ねじれ角の式の公式φ=θLについてです。比ねじれ角θは”単位長さあたりのねじれ角”とのことですので単位はradではなく、rad/mmではないでしょうか?
大変勉強になりました。ねじりは理解しにくかったので助かりました。