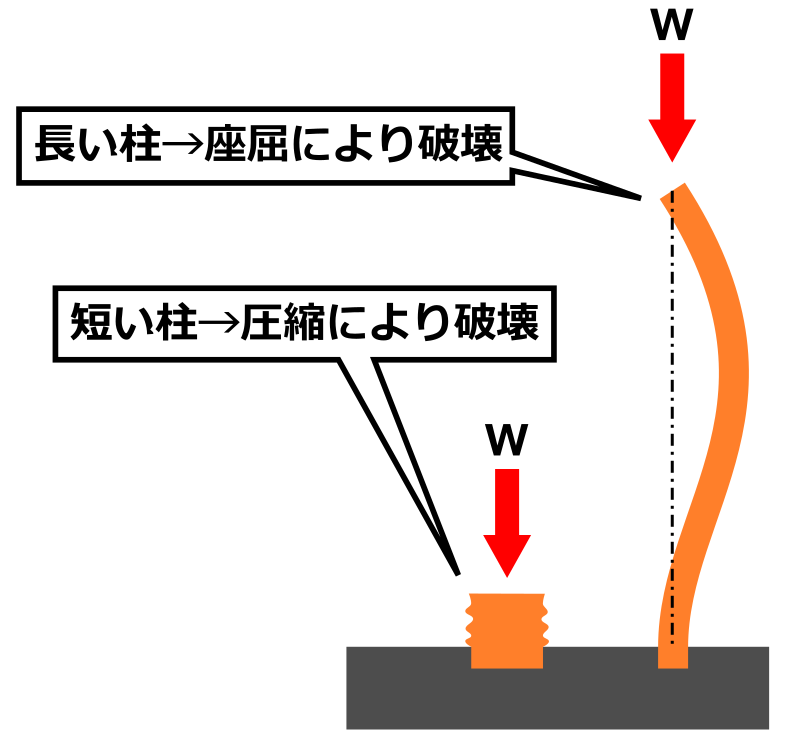
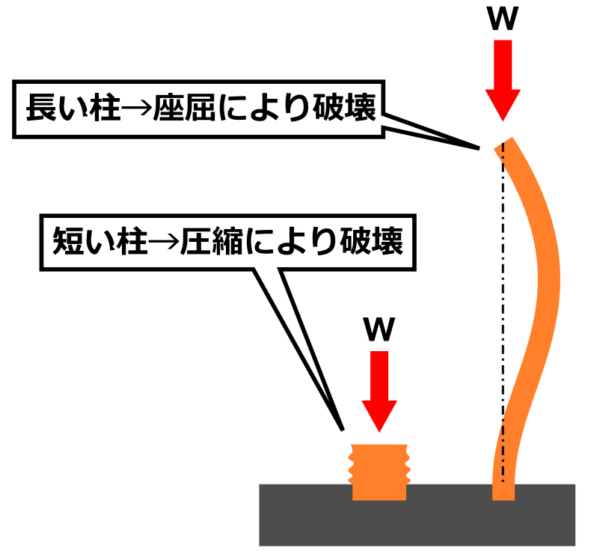
長い柱の軸方向に圧縮荷重がかかると、柱が圧縮によって潰れるより先にくにゃっと曲がってしまいます。これを座屈といいます。
柱が座屈により破壊しないか?機械設計における強度計算方法について計算例を交えて説明します。
座屈以外の強度計算は下記の記事が参考になります。
この記事の目次
この柱は座屈する?座屈しない?
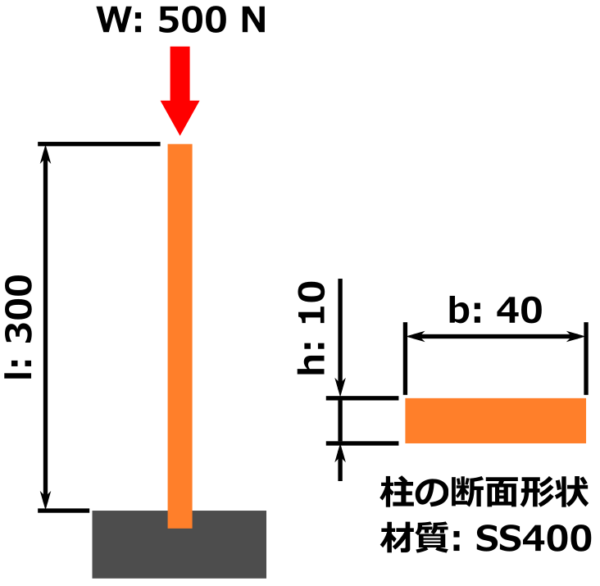
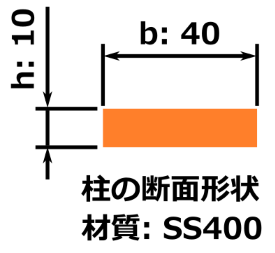
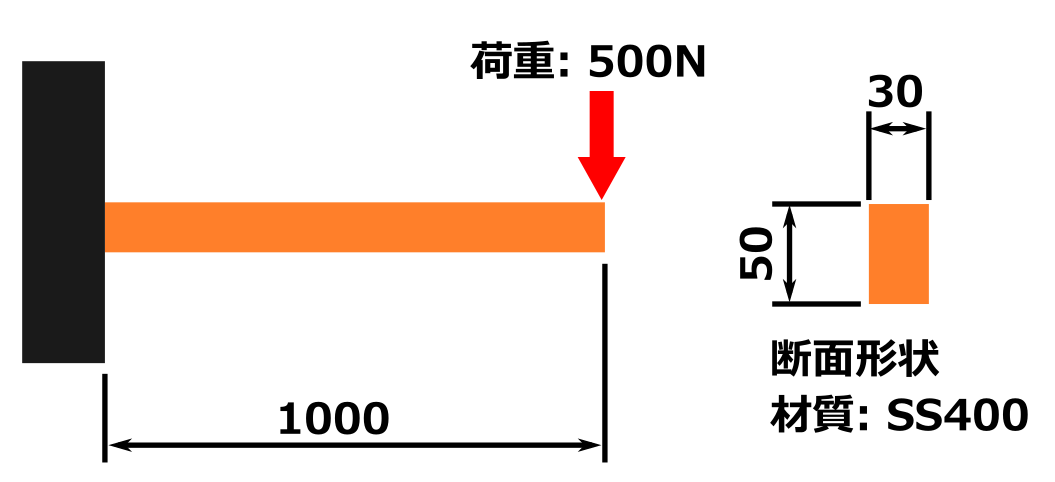
この図のような状況のとき、オレンジ色の柱は座屈してしまうのか?座屈しないのか?
ということを計算してみたいと思います。
- 部品の断面は 幅40 mm、高さ10 mmの長方形
- 柱の長さ300mm
- 柱の根本は地面に固定、上端は固定されてない自由端
- 材質:SS400
- 上から500 Nの圧縮荷重が加えられている
という条件です。
座屈の計算の概要
今回の計算では「ランキンの式」と「オイラーの式」というのを使って座屈する荷重(座屈荷重)を計算していきたいと思います。
座屈荷重を断面積で割ったものを「座屈強さ」、「座屈強度」、「座屈応力」などと呼び単位は「MPa(N/mm2)」がよく使われます。
座屈の計算は少々ステップが長いですが、全体像としては以下の手順となります。
- 柱の断面積を計算
- 最小断面二次モーメントを計算
- 最小断面二次半径を計算
- 細長比を計算
- 細長比より「ランキン式」、「オイラーの式」どちらを適用するか判断
- 「ランキン式」または「オイラーの式」を用いて座屈荷重を計算
- (必要であれば)座屈強さ(座屈応力)を計算
ちなみに座屈荷重を計算するために必要なパラメーターは以下となります。
設計時に決める必要がある条件とも言えます。
- 断面形状、寸法
- 柱の長さ
- 材質
- 両端の条件
- 材料の縦弾性係数
[mntyzer_topmedium]
細長比の計算
では座屈強度の計算について詳しく説明していきます。
まず計算方法を一通り説明し、次に例題を実際に計算してみる、という記事構成にしています。
まず「細長比」を計算するんですが、
- 断面形状、寸法より「断面積」と「断面二次モーメント」を計算
- 断面積と断面二次モーメントより「断面二次半径」を計算
- 断面二次半径と柱の長さより「細長比」を計算
という流れとなります。
細長比と材質より、一定の値未満なら「ランキンの式」、一定以上なら「オイラーの式」を使用します。
断面積の計算
柱の断面形状より、断面積を計算します。
例えば長方形断面なら、面積を求める公式は小学校で習った下記ですね。
| A | 断面積 [mm2] |
|---|---|
| b | 断面の幅 [mm] |
| h | 断面の高さ [mm] |
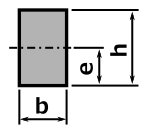
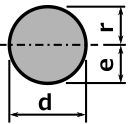
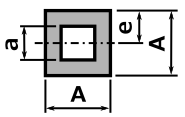
以下に主な断面形状の断面積の求め方を以下に示します。
計算した断面積はこの後使います。
|
断面 |
断面積 A |
重心の距離 e |
断面二次モーメント I |
断面係数 Z = I / e |
 |
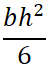 |
|||
 |
||||
 |
 |
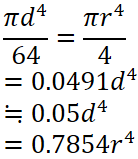 |
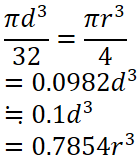 |
|
 |
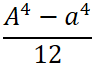 |
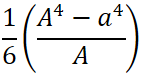 |
||
 |
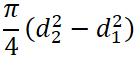 |
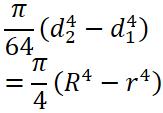 |
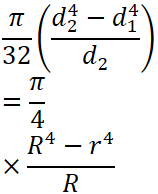 |
|
 |
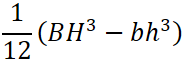 |
 |
最小断面二次モーメントの計算
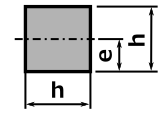
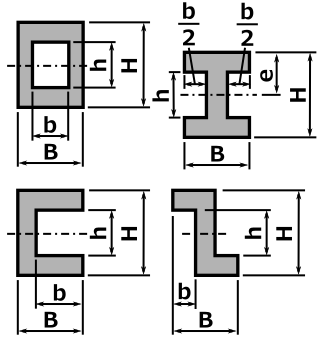
次に断面二次モーメントを求めるのですが、注意が必要なのは「最小断面二次モーメント」を求める点。
下の図ではbよりhの方が長くなってますが、このまま計算したら「最小」を求められないのでダメなんです。
正しくは下の図のようにb > hとなるように計算します。
長方形断面の断面二次モーメントの公式は下記ですが、分子の「h」を3乗してますよね。
| I | 断面二次モーメント [mm4] |
|---|---|
| b | 断面の幅 [mm] |
| h | 断面の高さ [mm] |
3乗しているhにbより大きい値を入れてしまうと、計算結果は大きな値となり、最小断面二次モーメントを求められなくなります。
断面形状が正方形や円の場合向きは関係ないですが、長方形はどの向きで計算したら断面二次モーメントIが最小となるか考える必要があります。
さっきと同じ表ですが主な断面形状の断面二次モーメントの求め方を以下に示します。
| 断面 | 断面積 A | 重心の距離 e | 断面二次モーメント I | 断面係数 Z = I / e |
 |
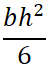 |
|||
 |
||||
 |
 |
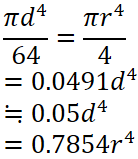 |
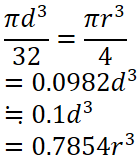 |
|
 |
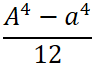 |
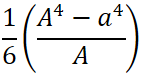 |
||
 |
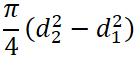 |
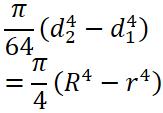 |
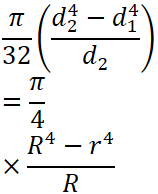 |
|
 |
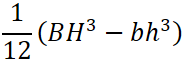 |
 |
最小断面二次半径の計算
断面二次半径を求めます。
「断面回転半径」、「回転半径」、「二次半径」などと呼ばれることもありますが、同じものです。
先ほど求めた「最小断面二次モーメント」を使って計算するので、ただの「断面二次半径」ではなく「最小断面二次半径」となります。
座屈の計算をする上で重要なパラメータです。
公式はこちら。
| κ (カッパ) | 最小断面二次半径 [mm] |
|---|---|
| I | 最小断面二次モーメント [mm4] |
| A | 断面積 [mm2] |
細長比の計算
柱の長さと最小断面二次半径の比を「細長比」といいます。
細長比の値が大きいと長い柱、小さいと短い柱を示しています。
| l/κ | 細長比 |
|---|---|
| l (小文字のエル) | 柱の長さ |
| κ (カッパ) | 最小断面二次半径 [mm] |
細長比と材質より、一定の値未満なら「ランキンの式」、一定以上なら「オイラーの式」を使用します。
その一定の値は端末の条件と材質より求めます。
| 端末条件 | 自由端 | 両端回転端 | 回転端固定端 | 両端固定端 |
|---|---|---|---|---|
| 曲がり方 |  |
 |
 |
 |
| 端末係数 | n=1/4 | n=1 | n=2 | N=4 |
| 木材 | 鋳鉄 | 鋼鉄 | 軟鉄 | |
|---|---|---|---|---|
| オイラーの式 | 60√n以上 | 80√n以上 | 85√n以上 | 90√n以上 |
| ランキンの式 | 60√n未満 | 80√n未満 | 85√n未満 | 90√n未満 |
(nは端末係数)
オイラーの式による座屈荷重の計算方法(長い柱向け)
ここまでの計算で「オイラーの式」、「ランキンの式」どちらを使うか決まりました。
オイラーの式での座屈荷重の計算方法を説明します。
この座屈荷重を超える荷重がかかると部材は座屈して破壊してしまいます。
オイラーの式は比較的長い柱に適用され、圧縮作用を無視し曲げ作用のみを考慮して計算されます。
そのため、短い柱に使ってしまうと材料の圧縮応力を超えるような非常に大きな荷重となり、あり得ない結果になってしまいます。
オイラーの式の公式は以下のとおり。
| W | 座屈荷重 [N] |
|---|---|
| n | 端末係数 |
| π (パイ) | 円周率 |
| E | 縦弾性係数 [MPa] |
| Imin (大文字のアイ) | 最小断面二次モーメント [mm4 |
| l (小文字のエル) | 柱の長さ [mm] |
断面二次モーメントの「I (大文字のアイ」と柱の長さ「l (小文字のエル)」を見間違えないよう注意しましょう。
端末係数n、最小断面二次モーメントImin、柱の長さlは細長比の計算のときに使用しましたね。
同じ数値を入れればOKです。
最小断面二次モーメントの記号がさっきまでIだったのがIminになってますが、気にしないでください。
同じです。
縦弾性係数 Eが初めて出てきました。
主な材質の縦弾性係数を下表に示しますので参考にしてください。
| 材質 | 縦弾性係数 E [Mpa(N/mm2)] |
| 軟鋼 | 206,000 |
| 鋼 | 216,000 |
| 鋳鉄 | 74,000 |
| 黄銅 | 78,000 |
| アルミニウム | 72,000 |
| 銅 | 118,000 |
そして座屈荷重Wを断面積Aで割ると座屈強さσ [MPa]を求められます。
| σ (シグマ) | 座屈強さ [MPa] |
|---|---|
| W | 座屈荷重 [N] |
| A | 柱の断面積 [mm^2] |
ランキンの式による座屈荷重の計算方法(短い柱向け)
お次は短い柱向けの「ランキンの式」について。
曲げ作用と圧縮作用の両方が考慮された計算結果となります。
オイラーの式を短い柱に適用すると、圧縮応力を超えるような座屈荷重となることがありますが、ランキンの式では圧縮応力を超える結果にはなりません。
ランキンの式の公式はこちら。
うっかり「1 (数字のいち)」と「l (小文字のエル)」を間違えないようにご注意を。
| W | 座屈荷重 [N] |
|---|---|
| σc | 圧縮応力 [MPa] |
| A | 柱の断面積 [mm2] |
| a | 定数 |
| n | 端末係数 |
| l (小文字のエル) | 柱の長さ [mm] |
| κ (カッパ) | 最小断面二次半径 [mm] |
定数aと圧縮応力σcは次の表から選択します。
| 定数\材料 | 軟鋼 | 硬鋼 | 鋳鉄 | 木材 |
|---|---|---|---|---|
| a | 1/7500 | 1/5000 | 1/1600 | 1/750 |
| σc | 330 | 480 | 550 | 50 |
座屈荷重Wを断面積Aで割ると座屈強さσ [MPa]を求められます。
| σ (シグマ) | 座屈強さ [MPa] |
|---|---|
| W | 座屈荷重 [N] |
| A | 柱の断面積 [mm2] |
例題を実際に計算してみよう!
今まで説明した公式に、例題の数値を当てはめていって実際に計算してみます。
断面積の計算
今回計算する例では、
b = 40 [mm]
h = 10 [mm]
なので、公式に代入して計算します。
というわけで断面積は400 mm2です。
断面積はこの後の断面二次半径の計算等で何度か使います。
最小断面二次モーメントの計算
断面二次モーメントを計算しましょう。
この数値は断面二次半径の計算で使います。
数値を公式に代入して計算すると、断面二次モーメントは3333.3 mm4となりました。
断面形状によって、断面二次モーメントの公式が変わってくるのでお間違えのないように。
最小断面二次半径の計算
今回の例では最小断面二次モーメントIが3333.3 mm4、断面積Aが400 mm2だったので公式に代入して計算します。
計算により最小断面二次半径κは2.89 mmということが分かりました。
最小断面二次半径は次の細長比を計算するために使います。
細長比の計算
細長比を計算して式の選択をします。
今回の例は柱の長さlが300 mm、最小断面維持半径κが先程の計算により2.89 mmでした。
細長比の式に代入して計算すると、細長比は103.92と分かりました。
算出した細長比にてオイラーの式かランキンの式かを判断するためにもう少し計算が必要です。。
端末の条件は「一端固定端他端自由端」となり下表より端末係数nは、「1/4」です。
| 自由端 | 両端回転端 | 回転端固定端 | 両端固定端 | |
| 曲がり方 |  |
 |
 |
 |
| 端末係数 | n=1/4 | n=1 | n=2 | N=4 |
材質はSS400、つまり「軟鋼」なので下表より、90√n以上であればオイラーの式、未満であればランキンの式が適用となります。
| 木材 | 鋳鉄 | 鋼鉄 | 軟鉄 | |
|---|---|---|---|---|
| オイラーの式 | 60√n以上 | 80√n以上 | 85√n以上 | 90√n以上 |
| ランキンの式 | 60√n未満 | 80√n未満 | 85√n未満 | 90√n未満 |
(nは端末係数)
計算すると45となりました。・・・①
細長比は103.92なので①以上となり、「オイラーの式」が適用となります。
オイラーの式による座屈荷重の計算方法(長い柱向け)
いよいよオイラーの式を使って座屈荷重の計算です。
端末係数n、最小断面二次モーメントIminは確認&計算済みなので、新たに必要になるパラメータは縦弾性係数Eです。
SS400の縦弾性係数は206×103となります。
公式に代入するパラメータを整理してみます。
| n | 1/4 = 0.25 |
|---|---|
| π | 円周率 3.14… |
| E | 206000 [MPa] |
| Imin | 3333.3 [mm4 |
| l (小文字のエル) | 300 [mm] |
公式にこの値を入れていきます。
ステップが多かったですが、この柱の座屈荷重がようやく計算できました。
この柱は18.8 kN以上の荷重で座屈します。
座屈強さも求めてみます。
例題では荷重 500 Nがかかっていましたが、この柱の座屈荷重は18825.4 Nもあり、全然余裕ということが分かりますね。
ランキンの式による座屈荷重の計算方法(短い柱向け)
今回の計算例では柱が比較的長かったためオイラーの式が適用されましたが、説明のためランキンの式でも計算してみます。
材質のSS400は軟鋼なので、次の表より定数 aは「1/7500」、圧縮応力σcは「330」を選択します。
| ↓定数 | 材料→ | 軟鋼 | 硬鋼 | 鋳鉄 | 木材 |
|---|---|---|---|---|
| a | 1/7500 | 1/5000 | 1/1600 | 1/750 |
| σc | 330 | 480 | 550 | 50 |
断面積や断面二次半径はすでに計算済みなのでその数字を代入していきます。
公式に代入するパラメータを整理したのが下表です。
| A | 400 [mm2] |
|---|---|
| a | 1/7500 = 0.000133 |
| σc | 330 [MPa] |
| κ (カッパ) | 2.89 [mm] |
| n | 0.25 |
公式に代入して計算します。
ランキンの式で計算した座屈荷重は19.5 kNとなりました。
座屈強さは以下になります。
オイラーの式とランキンの式の計算結果を比較してみましょうか。
| オイラーの式 | ランキンの式 | |
|---|---|---|
| 座屈荷重 [kN] | 18.8 | 19.5 |
| 座屈強さ [MPa] | 47.1 | 48.8 |
オイラーの式のほうが若干小さい値になってます。
つまり設計的にはオイラーの式を用いたほうが安全側に寄るということです。
今回のケースは本来オイラーの式が適用されるので妥当なところですね。
安全率を見込んだ許容荷重はいくらに設定する?
今までの説明で、オイラーの式やランキンの式を使って座屈荷重を計算できるようになりました。
でも座屈する荷重ぎりぎりで設計するわけにはいきませんよね。
適当な安全率を見込んで、ある程度の余裕を持って設計する必要があります。
安全率をいくらに設定するかは非常に難しい問題ですが、手元にある資料では静荷重の場合の目安として次の安全率の記載がありました。
| 軟鋼 | 5 |
|---|---|
| 鋳鉄 | 8 |
| 木材 | 10 |
「アンウィンの安全率」の静荷重の値より少し高めですね。
一つの参考としてみてはいかがでしょうか。
参考: アンウィンの安全率
| 材料 | 固定荷重 | 繰返し荷重(片振り) | 交番荷重(両振り) | 衝撃荷重 |
|---|---|---|---|---|
| 鋳鉄 | 4 | 6 | 10 | 15 |
| 軟鋼 | 3 | 5 | 8 | 12 |
| 鋳鋼 | 3 | 5 | 8 | 15 |
| 銅および合金 | 5 | 6 | 9 | 15 |
| 木材 | 7 | 10 | 15 | 20 |
| 石材・コンクリート | 20 | 30 | (25) | (30) |
ちなみに今回の例では座屈荷重は18825.4 Nに対して荷重が500 Nでした。
次の安全率の式に代入してみます。
安全率 37.7となり、荷重に対して充分な座屈強度を有していることがわかります。
逆に、安全率を5とした場合はいくらの荷重まで許容できるでしょうか?
安全率を5とした場合、静荷重の場合は3765 Nまで問題なく使用できます。
これがオーバースペックだったり軽量化する必要がある場合は、許容荷重が500 Nになるよう断面形状、サイズを見直すなどして設計変更することも出来ます。
材質がアルミのときはどうする?
オイラーの式とランキンの式を使って座屈荷重を計算してみましたが、ランキンの式には一つ困ったことがあります。
それは、材質によって選択するランキンの式の定数がありますが、「軟鋼」、「硬鋼」、「鋳鉄」、「木材」しかなく、アルミやステンレスの場合はどうすれば?ってなることです。
この定数は実験によって得られたもので、未知の材料の場合の数値は、実験をしないと分からないってことになります。
きっちりとするなら、実際にその材料を使ってどの程度の力で座屈するか実験するしかありません。
自動車や航空機など人命にかかわる機械では、そのようなことが行われているはずです。
実験によって得られたデータがその会社の設計力となるわけですね。
でも実験なんて出来ない場合が多いと思うので、そんな場合はどうするかというと、とりあえずオイラーの式を適用して計算するのも一つの手です。
アルミで座屈を考慮するものといえば、アルミフレームなんかがありますが、ミスミのアルミフレームの強度計算についてのページではオイラー式で計算しているようです。
オイラーの式は本来は比較的長い柱に適用するので、短い柱の場合座屈荷重が非常に大きな値となってしまう欠点があります。
その他、ランキン式のような定数を用いずに計算できる「ジョンソンの公式」というのがあり、ランキンの式の代わりにこちらを使用することもできそうです。
ジョンソンの式については、こちらの記事にて説明しています。
座屈強さが圧縮強さを超えると明らかにおかしい
オイラーの式しか使えない状況で、オイラーの式を用い短い柱を計算したとき、座屈荷重が異常に大きな値となってしまいます。
異常な値かどうかを判断する手として、座屈強さが材料の圧縮強さを超えていないか?と言う点を確認すればよいでしょう。
座屈強さσ [MPa]の式ですが、座屈荷重Wを断面積Aで割ることにより求めます。
| σ(シグマ) | 座屈強さ [MPa] |
|---|---|
| W | 座屈荷重 [N] |
| A | 柱の断面積 [mm^2] |
荷重を断面積で割るということは、圧縮強さ(圧縮応力)の計算と同じです。
つまり、座屈強さが圧縮強さを超えてしまっていたら、座屈するより先に部材は圧縮によって破壊されてしまいます。
すなわちその座屈荷重は異常な値だと判断できますね。
オイラーの式は曲げによる破壊のみ考慮しているので、短い柱の場合はこのようなことになってしまいます。
注意しましょう。
まとめ
座屈は次のステップで計算できます。
- 柱の断面積を計算
- 最小断面二次モーメントを計算
- 最小断面二次半径を計算
- 細長比を計算
- 細長比より「ランキン式」、「オイラーの式」どちらを適用するか判断
- 「ランキン式」または「オイラーの式」を用いて座屈荷重を計算
- (必要であれば)座屈強さ(座屈応力)を計算
座屈以外の強度計算は下記の記事が参考になります。

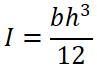

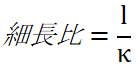
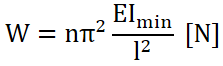
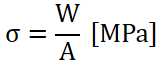
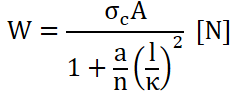
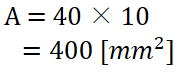
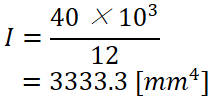
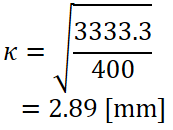
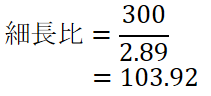
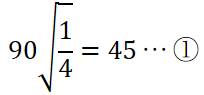
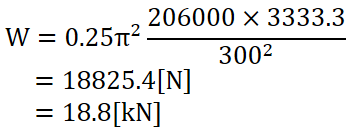
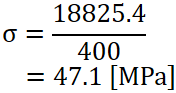
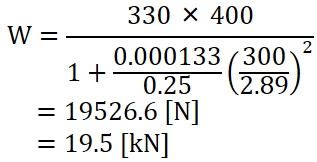
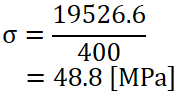

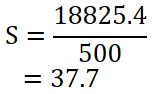
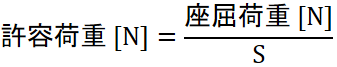
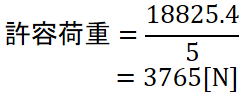
コメント