機械設計では「許容応力」を決めて、想定される応力が許容応力以下になるように部品を設計します。
その許容応力の求め方ですが、材料力学の教科書や参考書には詳しく説明がないことが多いです。
なぜなら、許容応力をいくらにするかは、設計者の主観が少なからず入る実務寄りな内容のため、教科書では説明しづらいんですね。
設計者を悩ます許容応力の求め方について説明したいと思います。
許容応力とは?
機械設計では各部材の許容応力を設定して寸法を決めます。
許容応力とは、設計上その部材に加えても大丈夫な応力となり、その値は設計者が決めるものです。
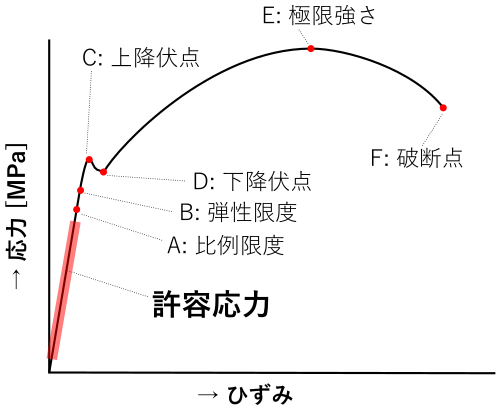
材料の持つ極限強さや降伏点などを基準強さとし、許容応力はそれより小さい値とします。
例えば引張強さ 400 MPa、断面積 1 mm2の部材があるとします。
この部材は400 Nで引っ張るとちぎれます。
想定される荷重が399Nだったとして、その部材を引っ張った時に部材に生じる引張応力は399 MPa。
- 引張強さ400 MPa > 引張応力399 MPa
よし、引張強さのほうが大きいからOKだ!
なんて設計者がいたら、素人目に見ても危険なニオイがプンプンしますよね。
わずか1 Nでも想定外の荷重が加わると破断してしまいます。
そうならないために、許容応力をいくらにするかを決めて、部材内部に発生する応力が許容応力以下になるように寸法を決めるわけです。
その許容応力をどうやって決めるのか?と言うのが今回のテーマとなります。
ちなみに、引張応力の計算方法については下記記事を参照してください。
[mntyzer_topmedium]
許容応力の決め方・基準強さと安全率を使う方法
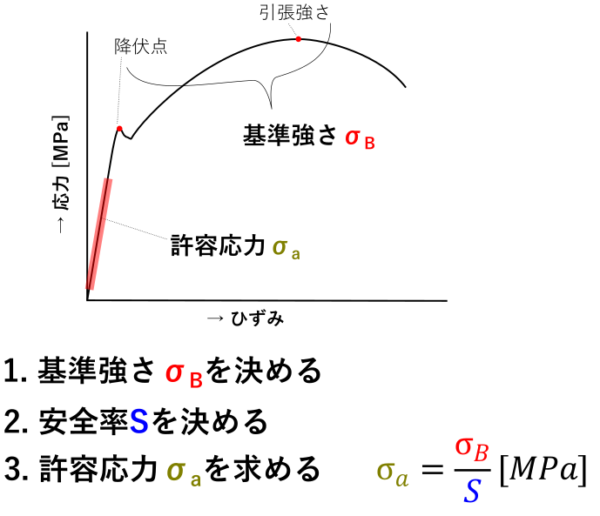
許容応力を決めるために使われるのが、「基準強さ」と「安全率」による考え方。
安全率を使って許容応力を求める式が下記になります。
\[\LARGE \sigma_a=\frac{\sigma_B}{S}[MPa] \]
| S | 安全率 |
|---|---|
| σB | 基準強さ [MPa] |
| σa | 許容応力 [MPa] |
基準強さを安全率で割ったものが許容応力となります。
じゃあ基準強さと安全率の値はいくらなの?となると思うので、順に説明していきます。
※注意
今回紹介する方法はあくまで一例です。
設計者や会社によって様々な考え方があり、画一的に決まった方法と言うのはありません。
基準強さを設定する(引張強さ、降伏点、疲労限度)
荷重の種類などを考慮して基準強さを決めます。
静的な荷重の場合は引張強さや降伏点を基準強さに設定します。
単に破断するかしないかに焦点を当てる場合は、引張強さを、
永久変形するかしないかに焦点を当てる場合は、降伏点(または0.2%耐力)を基準強さに設定します。
繰返し荷重の場合は疲労限度を設定しますが、各材料の疲労限度の数値を知ることが難しいため下記のようにします。
- 繰返し荷重(片振り): 引張強さ×2/3
- 繰返し荷重(両振り): 引張強さ×1/3
引張・圧縮・曲げ応力(総称して「垂直応力」)の場合は以上ですが、せん断応力やねじり応力の場合はさらに基準強さが小さくなり、\(\frac{1}{\sqrt3}\)を掛けた値とします。約0.6倍になります。
表にまとめるとこうです。
| 荷重の種類 | 応力の種類 | 基準強さ |
|---|---|---|
| 静荷重(破断を許さない) | 垂直応力 | 引張強さ |
| 静荷重(永久変形を許さない) | 垂直応力 | 降伏点(耐力) |
| 繰返し荷重(片振り)(破断を許さない) | 垂直応力 | \(引張強さ\times\frac{2}{3}\) |
| 繰返し荷重(両振り)(破断を許さない) | 垂直応力 | \(引張強さ\times\frac{1}{3}\) |
| 繰返し荷重(片振り)(永久変形を許さない) | 垂直応力 | \(降伏点(耐力)\times\frac{2}{3}\) |
| 繰返し荷重(両振り)(永久変形を許さない) | 垂直応力 | \(降伏点(耐力)\times\frac{1}{3}\) |
| 静荷重(破断を許さない) | せん断応力 | \(引張強さ\times\frac{1}{\sqrt3}\) |
| 静荷重(永久変形を許さない) | せん断応力 | \(降伏点(耐力)\times\frac{1}{\sqrt3}\) |
| 繰返し荷重(片振り)(破断を許さない) | せん断応力 | \(引張強さ\times\frac{1}{\sqrt3}\times\frac{2}{3}\) |
| 繰返し荷重(両振り)(破断を許さない) | せん断応力 | \(引張強さ\times\frac{1}{\sqrt3}\times\frac{1}{3}\) |
| 繰返し荷重(片振り)(永久変形を許さない) | せん断応力 | \(降伏点(耐力)\times\frac{1}{\sqrt3}\times\frac{2}{3}\) |
| 繰返し荷重(両振り)(永久変形を許さない) | せん断応力 | \(降伏点(耐力)\times\frac{1}{\sqrt3}\times\frac{1}{3}\) |
高い温度で使用する場合はクリープ限度を基準強さとする場合もあります。
各材料の機械的性質(引張強さ・降伏点(耐力))の調べ方について下記記事で説明しています。
安全率とは
安全率とは、基準強さ(引張強さなど)が許容応力の何倍か?と言う値のことです。
先程の説明の通り、基準強さを何に設定するかは状況により変わります。
そのため、安全率が同じでも基準強さが何なのか?によって許容応力はいくらでも変動します。
安全率と基準強さはセットで考えるようにしましょう。
安全率を大きくするほど荷重に対して壊れにくい頑丈なものになりますが、
- コストが上がる
- 重量が大きくなる
等デメリットもあります。
安全性とコストはトレードオフとなるため、最適な安全率を設定しないといけません。
安全だからといって、みんなが装甲車に乗るわけにはいきませんからね。
安全率を設定するということは、不確定な要素が存在するということです。
仮に400 MPaの応力までは絶対に壊れなくて、400 MPaを超える応力が絶対に生じないと断言できるのであれば安全率は「1」でも問題ないわけです。
しかし材料の欠陥や製造上の不具合、想定外の荷重や経年劣化等、不確定要素がいくつもあります。
そのような想定外の事態が起きても壊れないために安全率を設定します。
安全率は社内や業界のルールがあれば従う
安全率をいくらにするかですが、社内や業界のルールがある場合はそれに従いましょう。
安全率は各社独自に定めているのでその手の情報はあまり表には出てきません。
エレベーターのロープや建築物等は建築基準法などの法令で安全率が定められている場合もあります。
先ほど説明した基準強度を安全率で割ることで許容応力が求められます。
\[\LARGE \sigma_a=\frac{\sigma_B}{S}[MPa] \]
| S | 安全率 |
|---|---|
| σB | 基準強さ [MPa] |
| σa | 許容応力 [MPa] |
あくまで私が独自に調査した一例ですが、一般的な安全率を下表にまとめてみましたので参考にしてください。
安全率の例
| 品名 | 安全率 |
|---|---|
| 航空機 | 1.5 |
| ロケット | 1.15~1.25 |
| 一般機械部品 | 2~3 |
| 自動車の破壊 | 1.6 |
| 自動車部品の降伏や疲れ | 1.3 |
| 鉄骨構造 | 2.5~3.0 |
| エレベーターのロープ | 10以上 |
| クレーン | 8~10 |
| クランクシャフト | 40 |
| 原子炉圧力容器 | 3 |
| 化学プラント | 4 |
| 建築物 | 1.5 |
航空機やロケットは安全率を高くしすぎると重くて飛べなくなるので、低い値となっています。
どのように安全率を下げているかというと、
- 想定される荷重に対して正確に強度設計する
- 製造時の管理や検査の徹底により欠陥なく製造する
- 経年劣化する前に部品を交換する
等、信頼性を上げることで不確定要素を減らし、安全率を下げています。
重要な箇所は安全率を高めにする
例えばその部品が壊れたら人が死ぬ、みたいな重要な箇所は安全率を高めにします。
壊れても影響がない部品はコスト削減のため安全率を低めに設定します。
この辺は各設計者、各社のノウハウですね。
さっきの安全率の表で、クレーンは8~10と安全率が高めの値となっています。
破断は重大な事故につながるため、重量が増加しても安全性を高めたいという設計思想が見えてきますね。
目安がない場合はアンウィン(Unwin)の安全率を用いる
安全率の目安となるものが全く無い場合、「アンウィン(Unwin)の安全率」を利用することができます。
ただし、かなり古典的な手法で精度が良くない(安全率が大きすぎる)と言う意見もあります。
とはいえ、機械設計製図便覧にも掲載されている有名なものなので、使ってはダメなわけではありません。
アンウィンの安全率の表がこちら。
| 材料 | 固定荷重 | 繰返し荷重(片振り) | 交番荷重(両振り) | 衝撃荷重 |
|---|---|---|---|---|
| 鋳鉄 | 4 | 6 | 10 | 15 |
| 軟鋼 | 3 | 5 | 8 | 12 |
| 鋳鋼 | 3 | 5 | 8 | 15 |
| 銅および合金 | 5 | 6 | 9 | 15 |
| 木材 | 7 | 10 | 15 | 20 |
| 石材・コンクリート | 20 | 30 | (25) | (30) |
材料や荷重の種類により安全率が簡単に分かります。
先程基準強さの選択方法として、
- 静荷重(破断を許さない):「引張強さ」
- 繰返し荷重(片振り)(永久変形を許さない): 「降伏点(耐力)×2/3」
などと説明しましたが、アンウィンの安全率を使う時はこれは一旦忘れてください。
アンウィンの安全率では基準強さは引張強さとします。
表にあるように荷重の種類により安全率が変わるということは、繰返し荷重では疲労限度を見込んだ安全率となっていると思われます。
そのため、基準強さに「疲労限度」や「引張強さ×1/3」の値を使うと、過剰な安全率となってしまいます。
許容応力の設定例
許容応力より部品のサイズを決めるという設計の練習をしてみましょう。
例1
- 材質: SS400 (引張強さ 400 MPa、降伏点 245 MPa)
- 荷重の種類: 引張、片振り繰返し荷重
- 条件: 永久変形を許さない
- 安全率: 3
- 断面形状: 円形
- 荷重の大きさ: 500 N
と言う条件で部品の直径を決めてみましょう。
天井から丸棒が生えていて、先端に何かを吊るすようなイメージです。
500 Nの荷重なので、51 kgくらいです。
吊るしたり外したりするので片振り繰返し荷重となります。
基準強さを決める
永久変形を許さない条件なので、引張強さではなく、降伏点を元に考えます。
荷重の種類は引張の片振り繰り返しなので、基準強さは下記の計算により求めます。
\[\LARGE 基準強さ=降伏点\times\frac{2}{3}[MPa] \]
値を代入して計算すると、下記計算の通り基準強さは163.3 MPaとなりました。
\[\LARGE\begin{eqnarray} \sigma_B&=&245\times\frac{2}{3}\\ &=&163.3[MPa] \end{eqnarray}\]
許容応力を求める
基準強さ / 安全率で許容応力が求められるんでしたね。
安全率が3と決められているので、下記の計算の通り、許容応力は54.4 MPaと求まりました!
\[\LARGE\begin{eqnarray} \sigma_a&=&\frac{163.3}{3}\\ &=&54.4[MPa] \end{eqnarray}\]
部品のサイズを決める
許容応力が決まったので、それを設計に反映させていきます。
引張応力、荷重、断面積の関係は次の式となります。
\[\LARGE \sigma=\frac{W}{A}[MPa] \]
応力と荷重がすでに分かっているので、断面積を求めたい。
ということで変形して次の式にします。
\[\LARGE A=\frac{W}{\sigma}[mm^2] \]
荷重が500 N、許容応力が54.4 MPaなので式に代入して計算すると、必要な断面積は9.19 mm2とわかりました。
\[\LARGE\begin{eqnarray} A&=&\frac{500}{54.4}\\ &=&9.19[mm^2] \end{eqnarray}\]
部品の断面は円形なので、断面積 Aから直径 Dを求める式は次になります。
\[\LARGE D=\sqrt{\frac{4A}{\pi}}[mm] \]
計算すると、3.42 mmと言う結果になりました。
部品の直径が3.42mm以上になるよう、設計に反映させます。
\[\LARGE\begin{eqnarray} D&=&\sqrt{\frac{4\times9.19}{\pi}}\\ &=&3.42[mm] \end{eqnarray}\]
例2(アンウィンの安全率を使う例)
同じ例をアンウィンの安全率を使って計算してみましょう。
アンウィンの安全率の基準強さは引張強さを使うので、「400 MPa」。
軟鋼で繰返し荷重(片振り)なので安全率は「5」。
よって、許容応力σaは「80 MPa」となります。
\[\LARGE\begin{eqnarray} \sigma_a&=&\frac{400}{5}\\ &=&80[MPa] \end{eqnarray}\]
部品に必要な断面積は「6.25 mm2」。
\[\LARGE\begin{eqnarray} A&=& \frac{500}{80}\\ &=& 6.25[mm^2] \end{eqnarray}\]
計算すると、2.82 mmと言う結果になりました。
\[\LARGE\begin{eqnarray}
D&=&\sqrt{\frac{4\times6.25}{\pi}}\\
&=&2.82[mm]
\end{eqnarray}\]
許容応力の決め方・その他の方法
基本的には基準強さと安全率を設定する方法で許容応力を決めれば良いですが、他の方法も見ていきましょう。
実物で試験する
実際にものを作って破壊試験するのが一番確実です。
実際の使用時に近い状況の荷重を加え、破壊する荷重を測定します。
破壊荷重より基準応力を決め、安全率を設定すれば許容応力を求められます。
現実には何度も実物で試験をするのが難しいことも多いですが。
「機械設計製図便覧」等の資料で許容応力の値を確認する
機械設計者に愛用者が多い「機械設計製図便覧」の第4章「材料力学」に、材料の許容応力が記載されています。
軟鋼、硬鋼、鋳鉄、銅、りん青銅、青銅、黄銅と言ったざっくりとした材質しか載ってないですが、
- 引張
- 圧縮
- 曲げ
- せん断
- ねじり
の各種応力についてそれぞれ
- 静荷重
- 片振り繰返し荷重
- 交番荷重
の荷重種類ごとの許容応力が載っています。
アルミやステンレスについては記載がないですが、このような資料を参考にしても良いでしょう。
JIS「B8205 圧力容器の構造-一般事項」の許容応力を参考にする
JIS規格(日本産業規格)の「B8205 圧力容器の構造-一般事項」に各種金属材料の引張強さや降伏点、弾性係数のデータが掲載されています。
その中で温度ごと許容応力についての記載があります。
常温で、引張強さに対する安全率4と言う値になっているようです。
あくまで圧力容器に関する規格での許容応力のため、様々な荷重条件の一般機械部品にそのまま適用するのは難しいかも知れませんが、温度により許容応力がどのように変化するか、というのは参考になります。
まとめ
許容応力は次の手順で求められます。
- 基準強さを決める
- 安全率を決める
- 許容応力 = 基準強さ / 安全率
許容応力は設計者が決める値です。
仕様や規格で決まっている場合は別ですが、許容応力を決めるための基準強さを何にするか?安全率をいくらにするか?も設計者が決めるものです。


コメント