片持ばりなどに曲げる荷重が加えられたとき、もとに戻らないほど変形(永久ひずみ)が残ったり、破壊したりしないか、と言った機械設計における強度計算方法について計算例を交えて説明します。
曲げ以外の強度計算は下記の記事が参考になります。
はりに曲げ荷重が加わった時のたわみの計算方法は下記の記事で説明しています。
この記事の目次
何Nの荷重で破壊する?
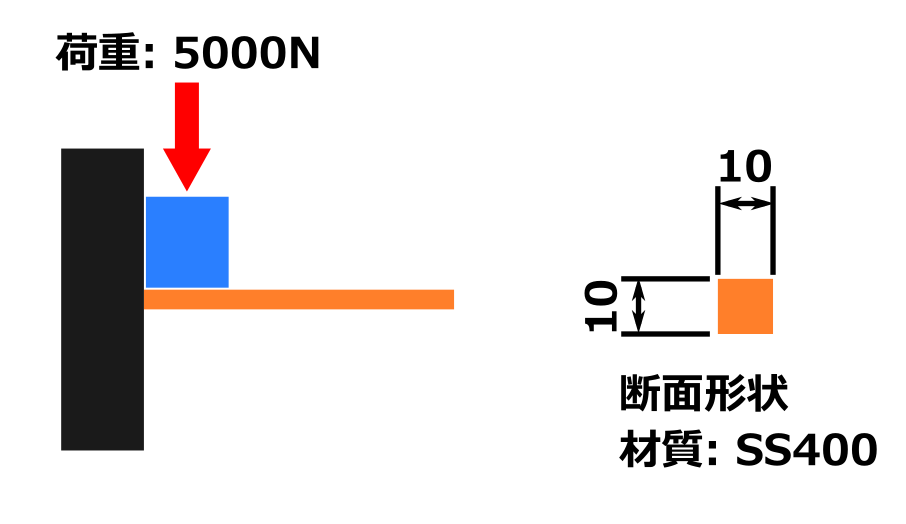
この図のような状況のとき、オレンジ色の部品は曲がったり壊れたりしないか?
またどのくらいの力で壊れるのか?ということを求めていきます。
- 部品の断面は 幅30 mm、高さ50 mmの長方形
- 材質:SS400
- 根本から1000 mmの位置に500 Nの荷重が加えられている
という条件です。
ここで言う「曲がる」と言うのは降伏強度を超える応力が発生して、荷重を取り除いても永久変形が残ると言う意味です。
加えられたのがわずかな荷重でも、部材は目に見えないほどわずかに弾性変形しています。(この例では「たわむ」と言ったほうが適当かもしれません。)
弾性限度内であれば、力を取り除くと元の寸法に戻ります。
機械設計において、永久変形は許されない場面が多く、どの程度の荷重で永久変形するかを計算して把握することはとても重要です。
片持ばりに1点の集中荷重が加えられるという単純な状況ですが、このような状況は現実に数多くあります。
クレーンのアームや、タイヤが取り付けられた車の車軸、フライパンの取手、等々。
これらを片持ばりと見なせば強度の計算が可能になります。
曲げに対する強度計算の概要
曲げに対する強さは以下のステップで計算出来ます。
- 曲げモーメントを計算
- 断面係数を計算
- 曲げ応力を計算
- 材料の降伏点、引張強さ、圧縮強さ等と曲げ応力を比較する
曲げに対する強さは荷重の位置や断面の形状によって計算が変わるので、引張やせん断に対する強度計算よりも少し手間がかかります。
曲げモーメントの計算方法
曲げモーメントとは物体を曲げるように働く力のこと。
そもそも「モーメント」というのが物体を回転させようとする力のことで、「トルク」と同じような意味になります。
曲げに対する強度計算において、この後出てくる「曲げ応力」を求めるために「曲げモーメント」を求める必要があります。
次の画像のように片持ばりに荷重がかかると、はりを曲げるように作用するので曲げモーメントとなります。

曲げモーメントの公式(片持ばり集中荷重)M=WL
| M | 曲げモーメント [N・mm] |
| W | 荷重 [N] |
| L | はりの根本から荷重までの距離 [mm] |
今回の例は長さ1000 mmの片持ばりの先端に500 Nの荷重がかかっているので、曲げモーメントの公式に代入すると以下の計算となります。
M = 500 × 1000
= 500000 [N・mm]
断面係数の計算方法
次に「断面係数」を計算します。
断面係数とは、はりの断面形状によって決まる値です。
数値が大きいほど曲げモーメントに対して強いはりと言えます。
「曲げ応力」を求めるために「断面係数」の値が必要になります。
形状によって断面係数の公式が変わってくるんですが、今回強度計算するはりは長方形断面という設定です。
今回計算する例では、
b = 30 [mm]
h = 50 [mm]
なので、公式に代入して計算します。
\[\LARGE\begin{eqnarray}
Z&=&\frac{1}{6}\times30\times{50}^2\\
&=&12500
\end{eqnarray}\]
今回の形状の断面係数Zは「12500」ということがわかりました。
ちなみに計算式を見てもらえば分かりますが、高さhを2乗しています。
つまり部品の強度を上げる必要がある時、材料の幅を増やすより高さを増やしたほうが圧倒的に効果が高いことを意味します。
幅を2倍しても断面係数は2倍になるだけですが、高さを2倍にすれば2の2乗で4倍になります。
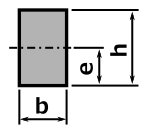
主な断面の断面係数一覧を下表に示します。
重心の距離とか断面二次モーメントとかも記載していますが、今必要なのは右端の断面係数です。
|
断面 |
断面積 A |
重心の距離 e |
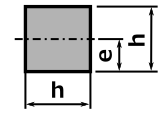
断面二次モーメント I |
断面係数 Z = I / e |
 |
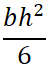 |
|||
 |
||||
 |
 |
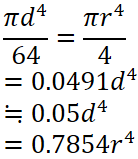 |
 |
|
 |
 |
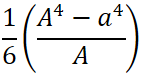 |
||
 |
 |
 |
 |
|
 |
 |
 |
他の断面形状の断面係数についてはいずれ他記事で解説したいと思います。
すぐ知りたい人は「断面係数」で検索してみてください。
曲げ応力の計算方法
曲げ応力は次の公式で計算できます。
先程の計算で曲げモーメントMと断面係数Zは以下の値でしたね。
M = 500000 [N・mm]
Z = 12500
これを曲げ応力の公式に代入します。
\[\LARGE\begin{eqnarray}
\sigma_b&=&\frac{500000}{12500}\\
&=&40\ [MPa]
\end{eqnarray}\]
というわけで、今回の例で部材に発生する曲げ応力は40 MPaということが分かりました。
材料の降伏点、引張強さと曲げ応力を比較する
部品に発生する曲げ応力を計算できましたが、「計算したけどそれで?」ってなりますよね。
Webにある強度計算の情報はここで終わっていることが多い気がします。
計算結果の40 MPaをどう判断したらいいのか?ってのが書いてないんですね。
当たり前すぎて書いてないのかもしれませんが、算出した曲げ応力は、材料の降伏点(降伏強度)や引張強さと比較し、以下のように判断します。
- 引張強さ > 曲げ応力 → 破壊しない
- 引張強さ < 曲げ応力 → 破壊される
曲げ応力と比較する値に降伏点を用いるか、引張強さを用いるかですが、永久変形を許さないのか、破壊を許さないのか、と言う基準で選択すればよいでしょう。
永久変形を許さない場合は降伏点を基準に考えます。
「降伏点 < 曲げ応力」となると荷重を取り除いても永久変形が残るので、それ以下の応力で使用する。
破壊を許さない場合は引張強さを基準に考えます。
「引張強さ < 曲げ応力」となるとポッキリ折れてしまうので、それ以下の応力で使用する。
と言った具合です。
今回強度計算する例では、曲げ応力が40 MPaでした。
材質がSS400なので、引張強さを 400MPaとします。
引張強さ 400 [MPa] > 曲げ応力 40 [MPa] なので、「部材は壊れない」ということが分かります。
片持ばりは根本から曲がる・危険断面について
曲げ応力が降伏強度を超えると永久変形すると言っても、どこが曲がるのでしょうか?
曲げモーメントを受けたはりは「危険断面」の位置で破壊します。
危険断面とは最大の曲げモーメントを受ける断面のこと。
片持ばりの危険断面がどこかというと、はりの根本です。
最大曲げモーメントをどこで受けるかを視覚的に知るには曲げモーメント図を書く必要があります。
下の図は片持ばりの曲げモーメント図(B.M.D)ですが、根本で最大曲げモーメントを受けていますね。
でもとりあえず「片持ばりは根本から曲がる」と覚えておけばOKでしょう。
曲げ応力とは
説明が後追いになってしまいましたが、そもそも曲げ応力とは何なのでしょうか?
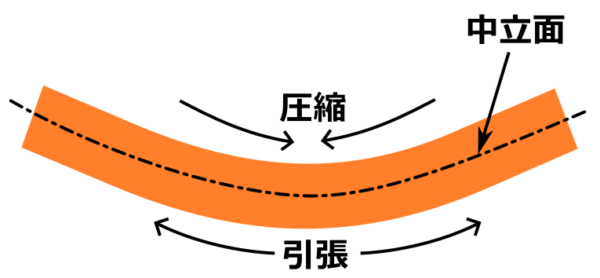
部材を曲げる力を加えると材料内部に引張応力と圧縮応力が生じる。これを総称して曲げ応力と呼びます。
断面の重心位置である中立面には応力が生じていません。
だから曲げ応力が発生する部品が壊れるか判断する時に引張強さと比較するんですね。
曲げ応力は材料内部に引張応力 + 圧縮応力が生じているので、曲げ応力が引張強さを超えると材料表面から破れて破壊するというわけです。
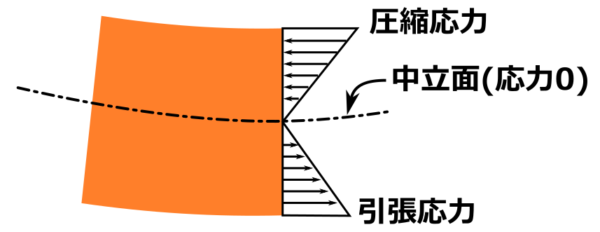
断面形状が長方形のように上下対称の場合は、部材に発生する圧縮応力と引張応力は等しくなります。
しかし断面が三角形やT字型やL型の場合、圧縮と引張の応力が異なってきます。
軟鋼は引張強さと圧縮強さを同等と見積もっても問題ありませんが、鋳鉄のように引張強さのほうが小さい材料の場合は、部材をどの向きで使うか注意が必要です。
具体的には「T字型」で使うか、Tをひっくり返した「逆T字型」で使うかと言った感じです。
荷重のかかり方を考え、Tの横棒がある側を引っ張りで受けるようにすればより有効となります。
各材料の降伏点、引張強さ、圧縮強さ
いくつかの金属材料の降伏点(または耐力)と引張強さをまとめてみました。
発生する曲げ応力が降伏点や引張強さを超えると、部材は永久変形したり破壊したりします。
| 種類 | 記号 | 降伏点または耐力 N/mm2 (= MPa) | 引張強さ N/mm2 (= MPa) |
|---|---|---|---|
| 一般構造用圧延鋼 | SS400 | 245 | 400~510 |
| 機械構造用炭素鋼 | S45C | 345 | 570 |
| ステンレス | SUS304 | 205 | 520 |
| ステンレス | SUS430 | 205 | 420 |
| アルミ合金 | A5052(質別: O) | 65 | 170~215 |
| 超々ジュラルミン | A7075(質別: T6) | 240~460 | 360~545 |
| ねずみ鋳鉄 | FC200 | – | 200以上 |
| タフピッチ銅 | C1100(質別: O) | 69以上 | 195以上 |
| 黄銅 | C2801 | – | 325~470以上 |
| 樹脂 | ABS | – | 61 |
| 樹脂 | PP | – | 35 |
| 樹脂 | PE | – | 24 |
| 樹脂 | PMMA | – | 67 |
| 樹脂 | PC | – | 61 |
| 樹脂 | PA66 | – | 82 |
※あくまで参考値です。実際に設計する際はJIS規格、樹脂メーカーのデータシート等でしっかり確認してください。
熱処理の仕方や、樹脂のグレードや温度によって値はいくらでも変わってきます。
曲げ応力は圧縮応力と引張応力が発生していると先程説明しましたが、こちらの表には「圧縮強さ」がありません。
降伏点や引張強さは調べたら数値が出てくることが多いですが、圧縮強さはあまり情報がないんですよね。
鋳鉄は別ですが、一般的な鋼は引張強さと圧縮強さは同等と考えて計算します。(鋳鉄は圧縮強さの方が強い)
安全率について
部材に発生する曲げ応力が材料の引張強さ以下だったとしても、ぎりぎりの設計だと思わぬ外力で破損する可能性があります。
そこで、引張強さや降伏点に対して安全率を考慮して適切な許容応力を設定することが大切です。
破壊する応力に対して、許容する応力の余裕を何倍とるか、ということです。
安全率の公式は以下。
この公式の「極限強さ」には材料の降伏点や引張強さを、「許容応力」には計算した曲げ応力を代入すれば安全率が分かります。
安全率をいくらにするか、というのも諸説ありますが、簡便に用いられているのが下表の「アンウィンの安全率」。
安全率がこの表の値以上になるよう、発生する曲げ応力を下げる、つまり部材を太くしたり設計を変更します。
極限強さが大きい材料に変更することで安全率を稼ぐと言う手も。
| 材料 | 固定荷重 | 繰返し荷重(片振り) | 交番荷重(両振り) | 衝撃荷重 |
|---|---|---|---|---|
| 鋳鉄 | 4 | 6 | 10 | 15 |
| 軟鋼 | 3 | 5 | 8 | 12 |
| 鋳鋼 | 3 | 5 | 8 | 15 |
| 銅および合金 | 5 | 6 | 9 | 15 |
| 木材 | 7 | 10 | 15 | 20 |
| 石材・コンクリート | 20 | 30 | (25) | (30) |
今回計算した例では、曲げ応力40 MPaでした。
材質はSS400を想定していて、この材質の降伏点、引張強さは以下の値となっています。
※ SS400の強度はJISで規定されていますが、板厚によって数値が変わって来たりするので、実際の設計に利用するときはしっかり確認してください。
| 降伏点 | 245 MPa |
| 引張強さ | 400 MPa |
公式に当てはめて計算してみましょう。
極限強さに「引張強さ」を入れてみました。
\[\LARGE\begin{eqnarray}
S&=&\frac{400}{40}\\
&=&10
\end{eqnarray}\]
アンウィンの安全率の表でSS400は軟鋼にあたります。
荷重の種類を「固定荷重」とすると、安全率は表より3以上必要であることがわかります。
先程の計算で安全率は10だったので、固定荷重に対しては十分な強度があると考えられます。
仮に衝撃荷重が加わる場合は、必要な安全率が12以上となり、強度不足です。
部品の断面サイズを大きくしたり、材質を変更したり、設計の見直しが必要となります。
極限強さに「引張強さ」を入れると破壊に対する安全率、
極限強さに「降伏点」を入れると永久変形に対する安全率
となります。
機械部品において想定される荷重に対して永久変形が許されることはあまりないので、どちらかというと降伏点を用いて安全率を計算することが多いかもしれません。
許容応力のより詳しい求め方については下記記事で説明しています。
まとめ
曲げに対する強さは以下のステップで計算出来ます。
- 曲げモーメントを計算
- 断面係数を計算
- 曲げ応力を計算
- 材料の降伏点、引張強さ、圧縮強さ等と曲げ応力を比較する
さらに安全率を考慮して、良い感じの設計にしましょう。
曲げ以外の強度計算は下記の記事が参考になります。







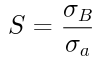

コメント
断面係数の計算で、最初「25」って書いていたのが「30」になっていて
計算は25でやっているので、30の表示が間違っています。
コメントありがとうございます。
本当ですね、図と本文が合ってなくて計算まで間違ってますね。
不整合のないよう修正しました。
わざわざ計算までして確かめていただきありがとうございます!
修正していただき、どうもありがとうございました。
今解析の勉強をしているので、このサイトはとても参考になります。
今後もよろしくお願いいたします。