【材料力学】引張荷重を加えた部品の変形量(伸び)の計算方法

機械設計において、部品の変形量を計算する機会は多々あります。
何Nの荷重を加えたらどれだけ変形するかの計算の仕方について説明します。
今回は最も基本となる、棒状の部材を引っ張ったら何mm伸びるか？について。

引っ張った時に破壊する強度を計算したい場合は下記記事を参考にしてください。

例題

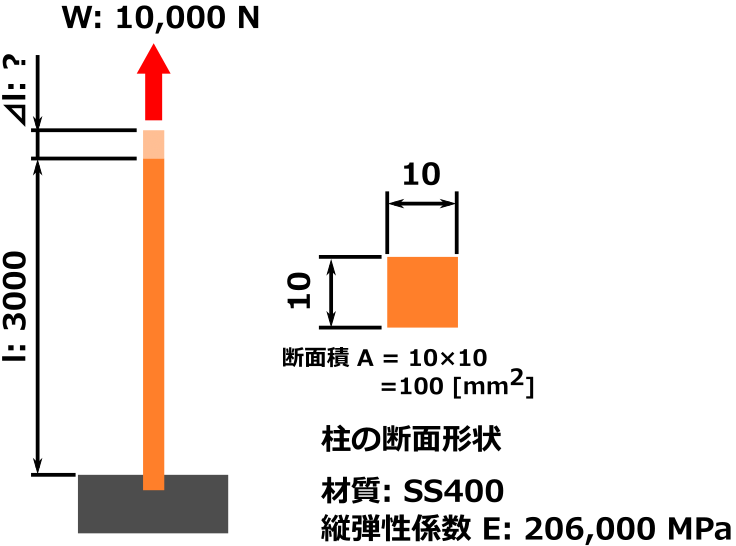
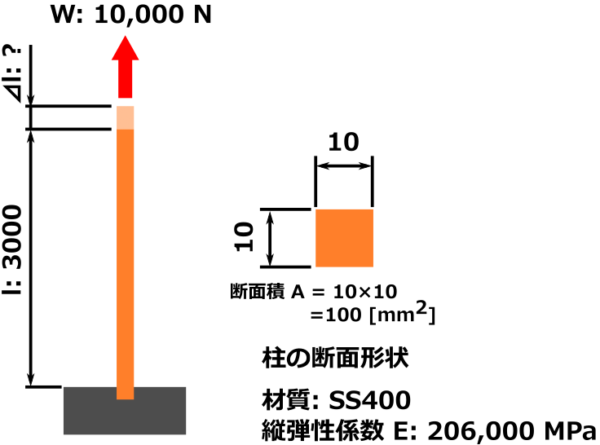
長さ3 m、1辺10 mmの正方形断面の棒に10 kN(=10,000 N)の引張荷重を加えた時、棒は何mm伸びますか？
丸棒の材質はSS400(縦弾性係数 E = 206 GPa)とする。

計算方法の概要

部材の寸法と加えられる荷重が分かっていて、変形量(伸び)を知りたい場合は下記の手順で計算できます。

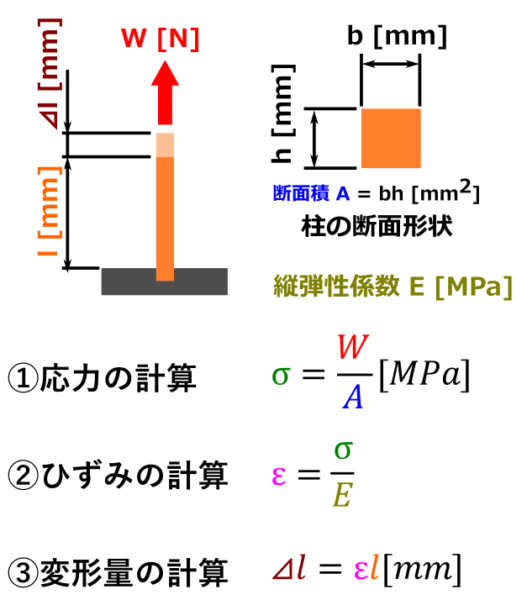
1. 応力を計算する
2. ひずみを計算する
3. ひずみから変形量を計算する

まずは計算方法の詳細を説明して、その後で例題を具体的に計算していきましょう。

引張荷重を加えた部品の変形量(伸び)の計算方法の詳細

部品の変形量(伸び)の計算方法の詳細です。
引っ張った場合は｢伸び｣ですが、圧縮した場合は同じ計算で｢縮み｣も求められます。

応力を計算する

伸びを計算するためにまずは部材に発生している応力を計算する必要があります。
応力とは、荷重に抵抗仕様と部材内部に生じる力のことで、単位面積あたりの荷重に等しくなります。
今回の例のように、単純に引っ張ったり圧縮した場合の応力を特に「垂直応力」と呼びます。

応力 σは加えられている荷重 Wを断面積 Aで割ると求められます。

ひずみを計算する

つぎに「ひずみ」を計算します。
ひずみとは、物体がどれほど変形しているかの割合を表します。
先程計算した応力 σを縦弾性係数 Eで割るとひずみ εが求まります。

ひずみに単位はありません。

さてここで唐突に「縦弾性係数」というのが出てきました。
これが何かは後ほど説明しますが、材料ごとに決まっている特有の値です。
ネットやJIS規格等で各材料の縦弾性係数を調べる事が出来ます。

各材質の縦弾性係数一覧

先程のひずみの計算で縦弾性係数を使用しました。
これの具体的な値がいくらかという例が下表となります。

材質	縦弾性係数 E [Mpa(N/mm2)]
軟鋼	206,000
鋼	216,000
ステンレス(SUS304)	186,000
リン青銅	120,000
アルミニウム(A5052)	72,000
銅(C1100)	118,000

縦弾性係数の単位として、上の表では[MPa(N/mm²)]としていますが、資料によっては[GPa]で表記されていることも多いです。

例えば軟鋼の値で下記の2つは同じです。

• 206,000 [MPa]
• 206 [GPa]

調べた縦弾性係数の単位がGPaだった場合は、数値を1000倍してMPaに換算してください。

ひずみから変形量(伸び)を計算する

ようやく変形量(伸び)が計算できます。
計算したひずみともとの長さをかけ算すると変形量となります。

お疲れさまでした。

例題を実際に計算してみる

では先ほど説明した計算方法に、例題の数値を当てはめていって実際に計算してみましょう。
改めて、例題がこちら。
この部材が何mm伸びるか計算します。

応力を計算する

今回の例題で与えられたパラメーターは下記になります。

W	10,000 [N]
A	100 [mm2]

式に代入して計算すると以下の計算の通り、応力は100MPaとなります。

ひずみを計算する

今回の例題で与えられたパラメーターは下記になります。

σ(シグマ)	100 [MPa]
E	206,000 [MPa]

式に代入して計算すると以下の通り、ひずみは0.000485となります。

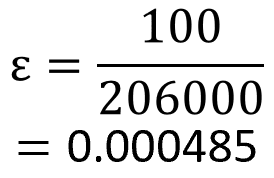
ひずみから変形量(伸び)を計算する

式に代入するパラメーターは下記になります。

ε(イプシロン)	0.000485
l	3000 [mm]

式に代入して計算すると以下の通り、部材の変形量(伸び)は1.46 mmということが分かりました！

この計算が使える範囲とフックの法則

今回の部材に引張(または圧縮)荷重を加えたときの伸び(縮み)の計算ですが、どんなときでも使えるわけではありません。
例えば、荷重をどんどん増やしていったら、計算上は伸びが10 mとかになりますが、現実はそんなに伸びる前に破断すると感覚的に予想できますよね？

この計算が使えるのは厳密に言うとひずみが比例限度以下の時のみ。(文献によっては比例限度と弾性限度を区別していない場合も。)
実際には各材料の比例限度がいくらなのかを知るのは難しいので、上降伏点以下なら成り立つと考えても、機械設計の現場としては大きな問題はないかと思います。

• 応力ひずみ線図

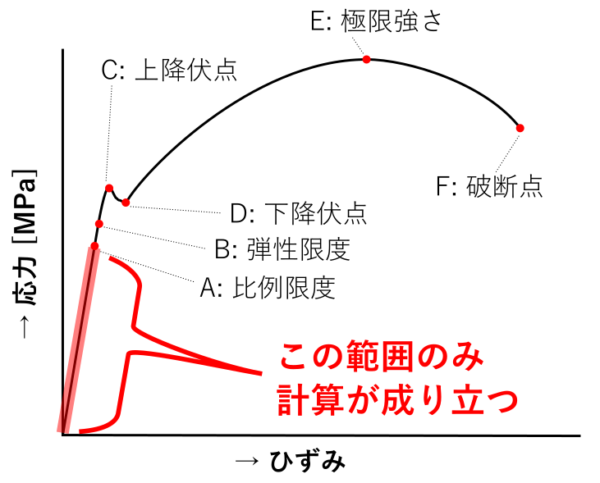
こうやって見ると、材料の変形を計算出来るのは、破断するまでの過程の内、最初のちょこっとだけですね。
この範囲より先は、応力に対するひずみを簡単に計算することができません。
本当に知りたければ、実際に使う材料で引張試験をしてデータを取るしかないって感じですね。

上の図で比例限度以下の範囲で成立するのが有名な｢フックの法則｣。
応力の値が比例限度を超えない範囲では、応力とひずみとの比は一定である、という法則です。
一応名前くらいは覚えておいて損はないかと思います。

縦弾性係数(ヤング率)とは？

計算の中で縦弾性係数というのが出てきました。
「ヤング係数」、「ヤング率」と呼ばれることもありますが、同じものです。
この縦弾性係数と言うのは、材料の変形のしにくさを表す数値です。
例えば軟鋼は206,000 MPa程度の値になりますが、数字が大きいほど変形しにくい材料と言えます。

アルミニウムは72,000 MPa程度と、軟鋼の1/3程。
つまり、同じ力を加えてもアルミは3倍くらい変形するということです。

先程の応力ひずみ線図の弾性限度以下でフックの法則が成り立つと書きましたが、この範囲内でのグラフの傾きが縦弾性係数になります。

• 縦弾性係数の値が大きい → グラフの傾きが垂直に近くなる → 同じ応力でもひずみ(変形)が少ない
• 縦弾性係数の値が小さい → グラフの傾きが寝てくる → 同じ応力でもひずみ(変形)が大きい

というわけです。

縦弾性係数と応力、ひずみのの関係は下記の式になります。

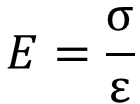
ひずみに単位がないので、縦弾性係数は応力と同じ単位(MPa、GPa)となります。

「縦弾性係数」は「ばね定数」に似た概念

ところで「ばね定数」って知ってますか？
物理の授業で習ったかもしれません。(私は習った記憶が一切ないですが。)
バネのカタログには必ず載ってて、「0.5 N/mm」などと書かれています。
これは、ばねに0.5 Nの力を加えると、バネが1mm縮むことを意味します。(圧縮コイルばねの場合)

10 N/mmのバネは1mm縮ませるのに10 N必要となり、数値が大きいほど硬いバネと言えます。
「縦弾性係数」もこの「ばね定数」と似た概念ですね。

すべての物体は、変形しない剛体ではなく、力を加えるとバネのように変形する。
ただし、変形量はごくわずかなので超硬いバネ！と考える事ができます。

断面積が一定じゃないと計算できない

今回の計算は、断面が途中で太くなったり細くなったりしたら計算できません。
段付きの丸棒とかなら、太さが同じ部分ごとに伸びを計算して足し算すると求めることができます。

なめらかに太さが変化している場合は、どうしたらいいでしょうか？

• 一番細い直径で伸びを計算したのを｢最大の伸び｣。
• 一番太い直径で伸びを計算したのを｢最小の伸び｣

として、実際の伸びは「最小の伸び」と「最大の伸び」の範囲内に収まる、位の目安は付けられるかと思います。

もっと複雑な形状になると、CAEを使って強度解析するのが現実的な解決方法となります。

まとめ

部材を引っ張った時の変形量(伸び)を知りたい場合は下記の手順で計算できます。

1. 応力を計算する
2. ひずみを計算する
3. ひずみから変形量を計算する

 - 材料力学