【材料力学】最大せん断応力の計算方法|長方形･円形･H型断面

2022/11/23 2023/02/05

材料力学の参考書では、せん断応力は荷重を断面積で割ると説明されていることが多いです。
でもこれ、実は「平均せん断応力」なんです。
つまり材料内部のには、平均せん断応力以上の応力が発生している領域があるということ。
今回は、長方形、円形、H型断面の最大せん断応力の計算方法を説明します。

平均せん断応力の計算については下記の記事で書いています。
今回の記事と合わせて読むと理解が深まるかと思います。

関連記事
【材料力学】せん断応力、せん断強度の計算方法

この記事の目次

1 最大せん断応力を計算する意味
2 復習平均せん断応力の計算方法
3 長方形断面の最大せん断応力計算方法
4 最大せん断応力は断面の中央に発生する
5 円形断面の最大せん断応力計算方法
6 H型断面の最大せん断応力計算方法
7 H型断面はせん断荷重を受けないほうが良い
8 まとめ

最大せん断応力を計算する意味

冒頭にも書きましたが、材料内部の特定の領域では、平均せん断応力以上の応力が発生している箇所があります。
計算した平均せん断応力が、材料の降伏点以下なのでOK！と思ってたら、部分的には降伏しているかもしれません。

実際には、十分な安全率を設定していれば、わざわざ最大せん断応力を計算しなくても問題ないと思います。
何らかの事情で、材料の降伏せん断応力ぎりぎりの設計だった場合は少し注意が必要ですね。

復習平均せん断応力の計算方法

下記の記事でも説明していますが、平均せん断応力の計算方法をおさらいしておきましょう。

関連記事
【材料力学】せん断応力、せん断強度の計算方法

以下の式のように、荷重を断面積で割ると平均せん断応力が求められます。

平均せん断応力の式

\[ \tau=\frac{W}{A}[MPa] \]

τ(タウ)	せん断応力 [MPa]
W	荷重 [N]
A	断面積 [mm²]

ここで計算したせん断応力が、材料の極限せん断強さを超えるとせん断破壊されます。
材料の極限せん断強さ、降伏せん断強さはJISにもはっきり書かれてないですが、引張強さ、降伏点の60%程度にするという考え方があります。

あくまで参考ですが、下表に各種材料のせん断強さなどを載せときます。

種類	記号	降伏点または耐力 N/mm² (= MPa)	引張強さ N/mm² (= MPa)	降伏せん断強さN/mm² (= MPa)	極限せん断強さN/mm² (= MPa)
一般構造用圧延鋼	SS400	245	400~510	147	240~306
機械構造用炭素鋼	S45C	345	570	207	342
機械構造用合金鋼	SCM435	785以上	930以上	471以上	558以上
ステンレス	SUS304	205	520	123	312
ステンレス	SUS430	205	420	123	252
アルミ合金	A5052(質別: O)	65	170~215	39	102~129
アルミ合金(超々ジュラルミン)	A7075(質別: T6)	240~460	360~545	144~276	216~327
タフピッチ銅	C1100(質別: O)	69以上	195以上	41.4以上	117以上
黄銅	C2801	–	325～470以上	–	195~282以上

長方形断面の最大せん断応力計算方法

では本題の、最大せん断応力の計算方法について。
まずは断面形状が長方形の場合です。

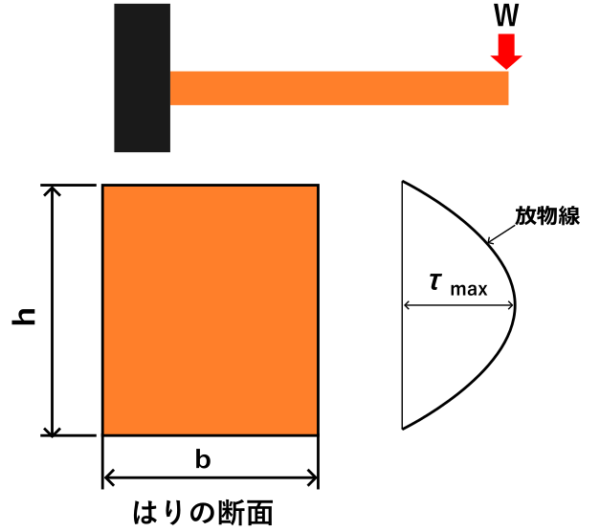
はりの断面の幅をb、高さをh、荷重をWとすると、次の式で最大せん断応力を求められます。

長方形断面の最大せん断応力の式

\[ \tau_{max}=\frac{3W}{2bh}=\frac{3}{2}\tau_{mean} \]

τ_max	最大せん断応力 [MPa]
τ_mean	平均せん断応力 [MPa]
W	荷重(せん断力) [N]
b	はりの幅 [mm]
h	はりの高さ [mm]

式から分かるように、要するに最大せん断応力は平均せん断応力の1.5倍となるわけです。

最大せん断応力は断面の中央に発生する

長方形断面の場合の最大せん断応力は平均せん断応力の1.5倍になるのは分かりましたが、どの箇所が最大となるのでしょうか？

上の図にも書いているように、内部に発生しているせん断応力の大きさは放物線状に変化し、中央で最大となります。
曲げ応力の場合は、最大応力が部材の上下の表面に現れるのとは対照的ですね。

円形断面、H型断面の場合も同じく中央で最大せん断応力が生じます。

円形断面の最大せん断応力計算方法

続いては円形断面の最大せん断応力の計算方法について。
計算式は下記になります。

円形断面の最大せん断応力の式

\[ \tau_{max}=\frac{4}{3}\tau_{mean} \]

τ_max	最大せん断応力 [MPa]
τ_mean	平均せん断応力 [MPa]

平均せん断応力と比較して4/3倍、つまり1.25倍の最大せん断応力が発生することになります。
長方形断面は1.5倍だったので、円形断面のほうが最大せん断応力が小さいですね。
断面積が同じで同じ荷重を受ける場合、どちらも平均せん断応力は同じですが、円形断面のほうが最大せん断応力が小さくなります。
円形断面のほうが、せん断荷重に対して強いと考えることができそうです。

H型断面の最大せん断応力計算方法

長方形断面や円形の断面の最大せん断応力を求める場合は、平均せん断応力を3/2倍や4/3倍してやればよいので簡単ですが、H型断面の場合はいきなりややこしくなります。
ちょっと私の理解の範囲を超えていてうまく説明出来ないですが、とにかく下の式で、中立軸からのy₁の位置のせん断応力が計算出来ます。
ウェブ部とフランジ部を別々に計算する必要があります。

ウェブ部のせん断応力の式
\[ \tau_w\left(y_1\right)=\frac{FS_z\left(y_1\right)}{I_zt}=\frac{F}{tI_z}\left\{\frac{t}{2}\left(\frac{h_2^2}{4}-y_1^2\right)+\frac{b}{8}(h_1^2-h_2^2)\right\} \]

τ_W(y₁)	y₁の位置のウェブ部のせん断応力 [MPa]
F	せん断力 [N]
h₁	全体の高さ [mm]
b	全体の幅 [mm]
t	ウェブの幅 [mm]
h₂	フランジ間の高さ [mm]
y₁	中立軸からの位置 [mm]
S_z(y₁)	y₁の位置の断面一次モーメント [mm³]
I_z	断面二次モーメント [mm⁴]

フランジ部のせん断応力の式
\[ \tau_F\left(y_1\right)=\frac{FS_z\left(y_1\right)}{I_zb}=\frac{F}{2I_z}\left(\frac{h_1^2}{4}-y_1^2\right) \]

τ_F(y₁)	y₁の位置のフランジ部のせん断応力 [MPa]
F	せん断力 [N]
h₁	全体の高さ [mm]
b	全体の幅 [mm]
t	ウェブの幅 [mm]
S_z(y₁)	y₁の位置の断面一次モーメント [mm³]
I_z	断面二次モーメント [mm⁴]

上記の計算に断面二次モーメントが必要ですが、H型断面の場合は次の式で計算できます。(上の図と寸法の取り方が違うので若干注意が必要です)

断面	断面二次モーメント I_z [mm⁴]
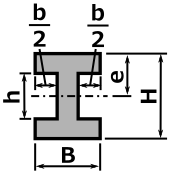	\[ \frac{1}{12}\left(BH^3-bh^3\right) \]

試しに適当な断面を設定し、エクセルで計算してグラフを書いてみるとこんな感じでそれっぽくなりました。

材料力学の学問的にはこの計算は正しくないとする説もあるようです。
しかし機械設計をする上でH型断面の最大せん断応力を計算する場合は、これで十分かと思います。

H型断面はせん断荷重を受けないほうが良い

H型断面は曲げ荷重を受けるのには向いていますが、最大せん断応力の計算から分かるように、せん断荷重を受けるのには向いていません。

最大せん断応力が中央部、つまり一番細いウェブ部に生じるので、断面形状的にH型は不利。
非常に短いはりの場合はH型断面じゃなく円形断面などのほうが有利となります。
H型を90°回転させると話はまた変わってきますが。

もちろん、設計している構造材にH型断面の鋼材が多用されていて、せん断荷重を受ける箇所にも同じH型を使うほうが合理的、という判断をするのも間違いではありません。

円形断面とH型断面どちらでも使える状況で断面積やらコストやらが同じなら、円形断面のほうがいいよね、という判断ができれば良いかと思います。

まとめ

十分な安全率を見越しておけば、わざわざ最大せん断応力を計算する必要はないかもしれません。
最大せん断応力を求めるのは、どちらかというと建築寄りの内容なのか、機械設計向けの材料力学の本にも最大せん断応力については載ってないことも多かったりします。

- 材料力学