前回の記事で1点集中荷重の両端支持ばりの支点の反力せん断力、曲げモーメント、せん断応力、曲げ応力の計算方法を説明しました。
今回は荷重が2点や3点など、複数の場合の計算方法を説明したいと思います。
せん断応力や曲げ応力については、せん断力や曲げモーメントを求めてしまえば1点集中荷重のときと同じ計算になるので、今回は詳細な説明を省略します。
また、前回の記事の内容を理解しているのを前提に、1点集中荷重と複数荷重の計算方法の違いを中心に説明します。
この記事の目次
両端支持ばり(複数荷重)の例
両端支持ばりが具体的にどのようなものかというと、小川に渡された丸太の橋を思い浮かべると分かりやすいかもしれません。
丸太の橋に一人乗っていると1点集中荷重、何人か乗っていると今回説明する複数荷重の両端支持ばりとなります。
例題
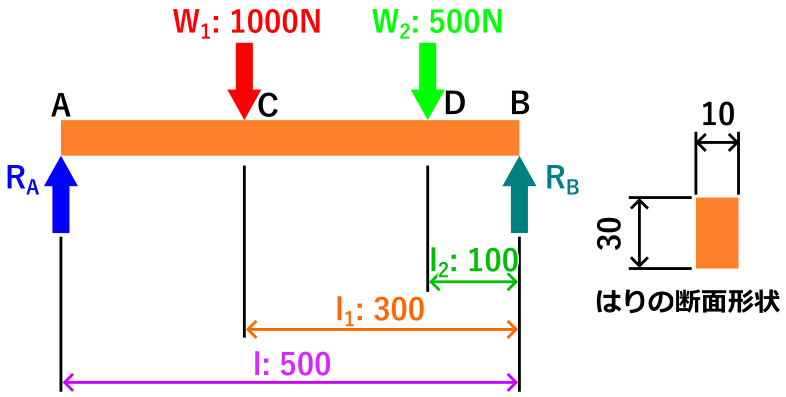
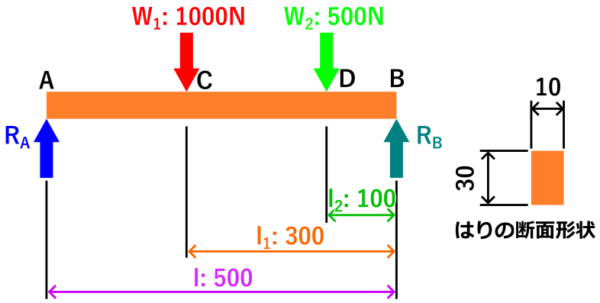
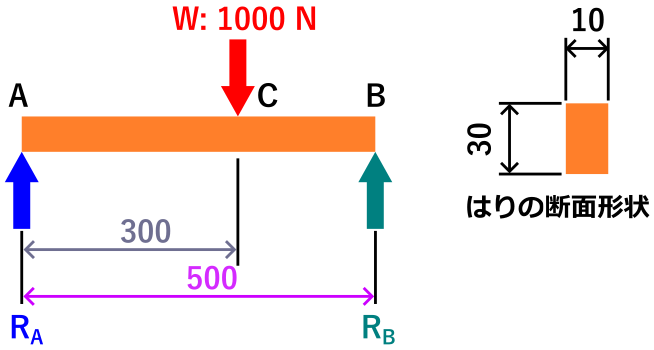
例題として下記のような状況のとき、このはりの強度は大丈夫なのか?ということを考えたいと思います。
この記事を読めばこれが解けるようになります。
材質はSS400とします。
まずは計算方法の説明をして、その後で例題を解いてみたいと思います。
両端支持ばり強度計算の概要
複数の荷重のある両端支持ばりの強度計算の全体像はこんな感じです。
次の章からそれぞれの詳しい計算方法を説明します。
③ 曲げモーメントの計算
④ せん断応力、曲げ応力を計算して材料の強度と比較して判断
④-1 せん断応力の計算
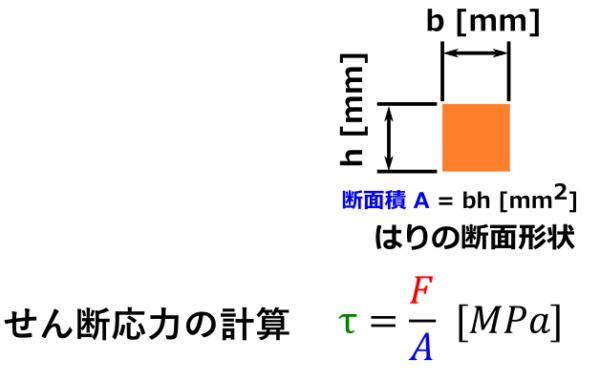
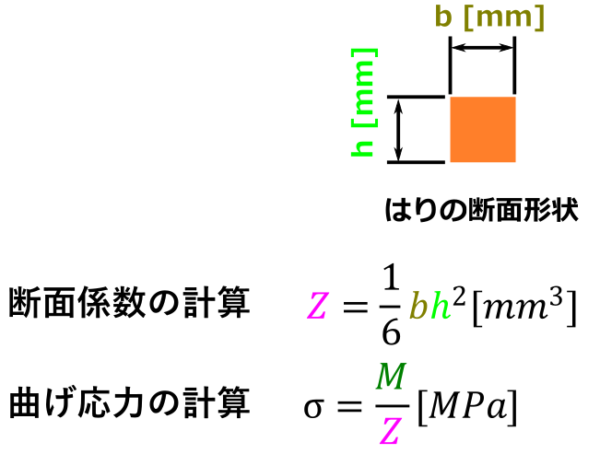
④-2 断面係数の計算
④-4 せん断応力、曲げ応力を材料の強度(引張強さ、降伏点)と比較して判断
計算方法の詳細
では、複数荷重ある両端支持ばりの強度計算の方法を詳しく見ていきましょう。
反力の計算・詳細解説
両端支持ばりの強度計算でまずやるべき事は、支点の反力の計算です。
せん断力や曲げモーメントを求めるときも、支点の反力が分からなければどうにもなりません。
そもそも支点の反力って何?って人もいるかも知れませんが、下の図で言うRA 、RBのこと。
はりを下から支える土台の部分がはりに与える力のことです。
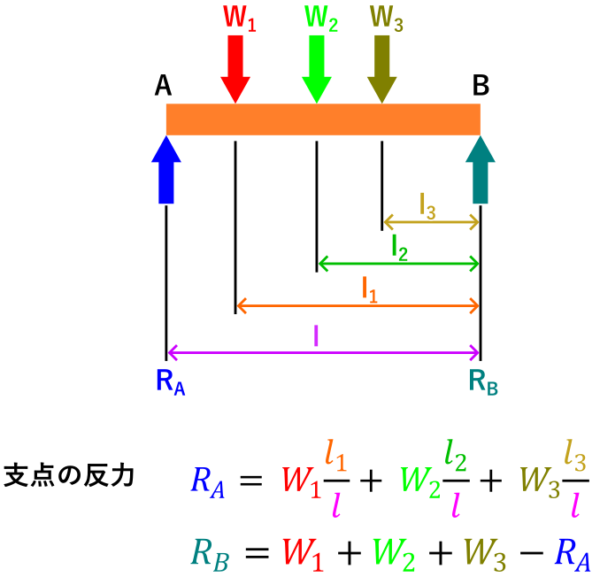
複数の荷重がある場合の支点の反力の計算方法は次の図のようになります。
反力の計算式
\[\LARGE R_A=W_1\frac{l_1}{l}+W_2\frac{l_2}{l}+W_3\frac{l_3}{l} \]
\[\LARGE R_B=W_1+W_2+W_3-R_A \]
| RA | 反力 [N] |
|---|---|
| RB | 反力 [N] |
| W1 ~ W3 | 荷重 [N] |
| l1 ~ l3 | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
\(W_1\frac{l_1}{l}\)に注目してみると、
W1は荷重で、\(\frac{l_1}{l}\)は荷重の位置をはりの全長に対する割合で表したものになります。
各荷重に対し、これらを掛け算したものをすべて足し算することで、支点の反力RAを求めることができます。
図では荷重が3つですが、荷重の数が4つ、5つと増えた場合も、同じ考えて足していけばOK。
RAを求める式は参考書によっては下記のように書かれていますが、式を変形すれば同じことです。
\[\LARGE R_A=\frac{W_1l_1+W_2l_2+W_3l_3}{l} \]
せん断力の計算・詳細解説
支点の反力を求めたら次はせん断力を求めましょう。
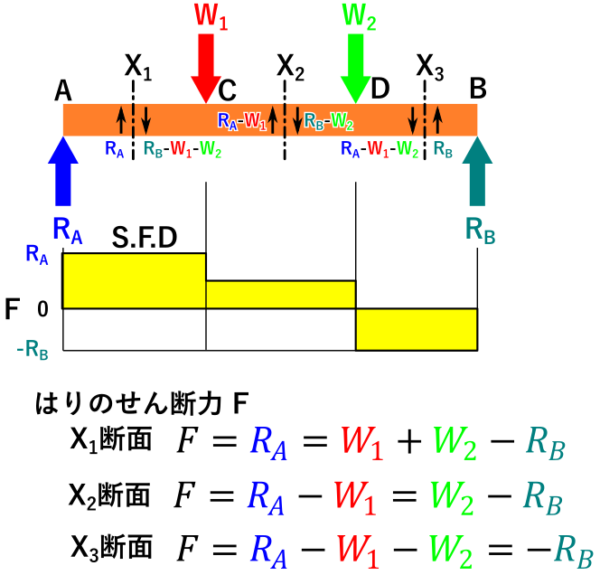
任意の断面から見て左側の、上向きの外力を正(+)、下向きの力を負(-)として合計することで、その断面に作用するせん断力を求められます。
外力の合計が上向きの場合はせん断力の符号が正(+)、下向きの場合は負(-)とします。
(正負の符号は、あくまでここではこうするというだけで、逆にしても問題ありません)
荷重が1箇所の場合と比べて、荷重の数が増えただけなので、「せん断力を知りたい任意の断面の左側の荷重を合計する」、と言う考え方は変わりません。
曲げモーメントの計算・詳細解説
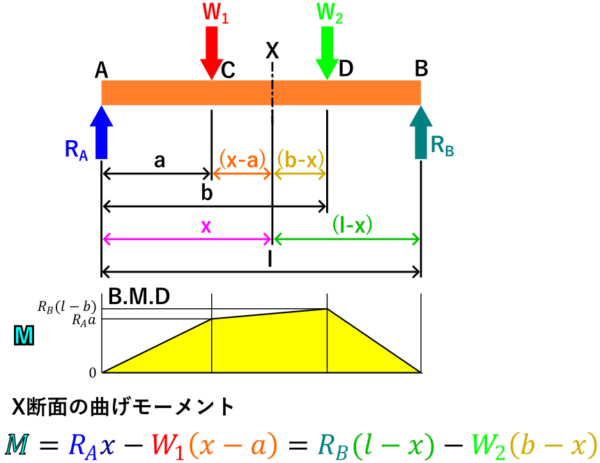
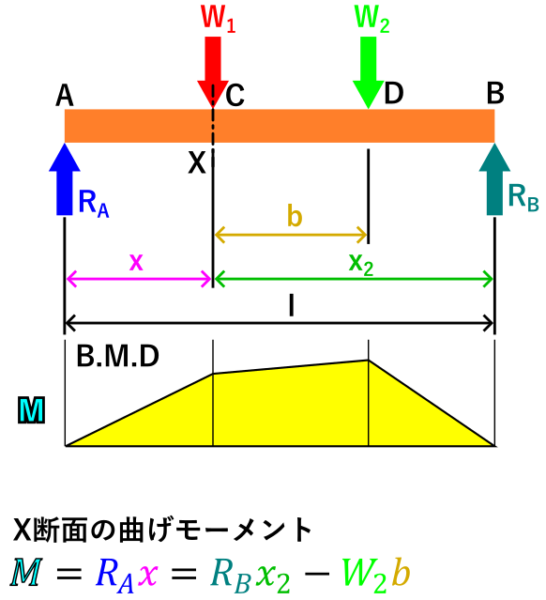
曲げモーメントをの計算は、曲げモーメントを知りたい断面(任意の断面X)から見て左側または右側の荷重と、X断面から荷重間の距離を掛け算を合計する、と言う考えかたです。
ただし任意の断面から見て左側のみ計算し、任意断面から見て時計回りのモーメントを正(+)、反時計回りのモーメントを負(-)として計算します。
はりの左側ではなく右側を計算する場合は時計回りのモーメントを負(-)、反時計回りのモーメントを正(+)とします。
はりのつりあい条件より、任意の断面の左側と右側のモーメントは同じ値となります。
なぜなら、左右のモーメントが同じじゃないとはりが動いてしまっている状態だからです。
はりが静止している前提で考えているので、左右のモーメントは同じ値となります。
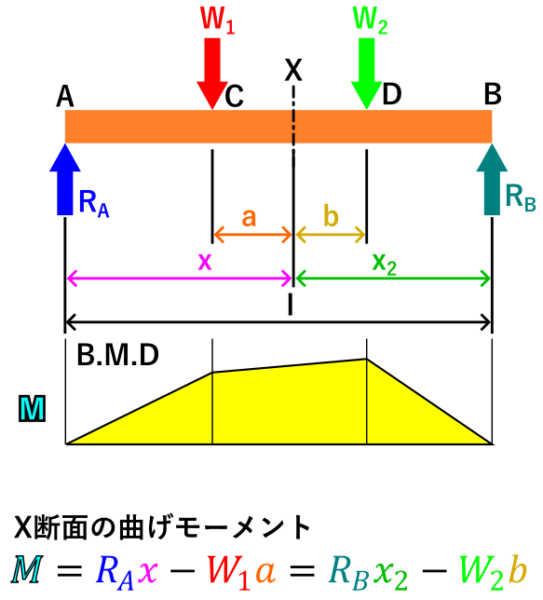
上と下の図は言ってることは同じですが、下の図のほうが「任意断面Xの左側(または右側)の、荷重と、X断面・荷重間の距離の積を合計する」と言う考え方としては分かりやすいかもしれません。
曲げモーメント図を見て分かるように、荷重の位置で傾きが変わっています。
なので、曲げモーメント図を書くために計算するときは、荷重の位置(点C, 点D)の曲げモーメントのみ計算すればOKですね。
例えば荷重W1の位置を断面Xとして曲げモーメントを計算したい場合、断面XとW1間の距離は0(ゼロ)なので計算する上ではW1は無視して下図のように計算出来ます。
せん断応力、曲げ応力の計算について
せん断力、曲げモーメントは部材の断面形状や断面のサイズに関わらず、はりの長さや荷重の大きさと位置により決まる値でした。
せん断応力、曲げ応力は部材の断面形状やサイズにより変わってくる値なので、求めるにはそれらの情報が必要になります。
せん断応力、曲げ応力の計算方法については、前回の記事で書いているのでそちらを参照ください。
前回の記事の1点集中荷重の両端支持はりと、複数荷重の両端支持ばりでは、せん断力、曲げモーメントの計算方法が少し違いましたが、それらを求めた後のせん断応力、曲げ応力の計算方法は同じになります。
例題の計算
では例題を計算してみましょう。
反力の計算
まずは反力の計算から。
例題の図から読み取った次の値を代入して計算します。
例題は荷重が2箇所なので、W3、l3はありません。
| 荷重W1 | 1000 [N] |
|---|---|
| 荷重W2 | 500 [N] |
| 荷重の位置 l1 | 300 [mm] |
| 荷重の位置 l2 | 100 [mm] |
| はりの長さ l | 500 [mm] |
反力RAについて計算してみると、700 Nということがわかりました。
\[\LARGE\begin{eqnarray} R_A&=&W_1\frac{l_1}{l}+W_2\frac{l_2}{l}\\ &=& 1000\times\frac{300}{500}+500\times\frac{100}{500}\\ &=&700\ [N] \end{eqnarray}\]
反力RBについても計算すると、800 Nとなりました。
\[\LARGE\begin{eqnarray} R_B&=&W_1+W_2-R_A\\ &=&1000+500−700\\ &=&800 [N] \end{eqnarray}\]
せん断力の計算
続いてせん断力の計算ですが、任意の断面から見て左側の、上向きの外力を正(+)、下向きの力を負(-)として合計することで、その断面に作用するせん断力を求められるんでしたね。
例題のAC間、CD間、DB間のせん断力を求めてみましょう。
計算式に、下記の値を代入して計算してみます。
| 反力 RA | 700 [N] |
|---|---|
| 反力 RB | 800 [N] |
| 荷重 W1 | 1000 [N] |
| 荷重 l2 | 500 [N] |
AC間のせん断力はRAの値そのものなので、計算するまでもなく700 Nです。
\[\LARGE\begin{eqnarray} F&=&R_A\\ &=&700\ [N] \end{eqnarray}\]
CD間のせん断力は計算の結果-300 Nとなりました。
\[\LARGE\begin{eqnarray} F&=&R_A-W_1\\ &=&700−1000\\ &=&−300 [N] \end{eqnarray}\]
DB間についてもRBの値そのままなので計算する必要はありません。
ただし、RBはDB間の任意断面から見て右側で上向きの力なので、符号が-(負)となることに注意が必要です。
\[\LARGE\begin{eqnarray} F&=&-R_B\\ &=&−800 [N] \end{eqnarray}\]
最大曲げモーメントの計算
続いて曲げモーメントの計算です。
どこの曲げモーメントを計算するかですが、荷重が加わる点C、点Dを計算してみましょうか。
計算したい場所(任意断面)の左側に作用するモーメントを合計すればOKです。
点Cの曲げモーメント計算は下記の通り140,000 N・mとなります。
\[\LARGE\begin{eqnarray} M&=&R_A\left(l-l_1\right) \\ &=&700\times\left(500-300\right) \\ &=&140000\ [N・mm] \end{eqnarray}\]
曲げモーメントを知りたい断面から見て左側のモーメントを合計すれば良いので反力RAについてのみ計算すればよいです。
点Cは荷重W1なので、点Cから見たW1の距離は0(ゼロ) mm。つまり1000 [N] × 0 [mm] = 0 [N・mm]となるので考えなくて大丈夫です。
点Dの曲げモーメント計算は下記の通り80,000 N・mとなります。
\[\LARGE\begin{eqnarray} M&=&R_A\left(l-l_2\right)-W_1(l_1-l_2)\\ &=&700\times\left(500-100\right)-1000\times(300-100)\\ &=&80000\ [N・mm] \end{eqnarray}\]
点Dから見て左側のモーメントを合計しています。
ここでは、点Dから見て時計回りのモーメントを正(+)、反時計回りのモーメントを負(-)としています。
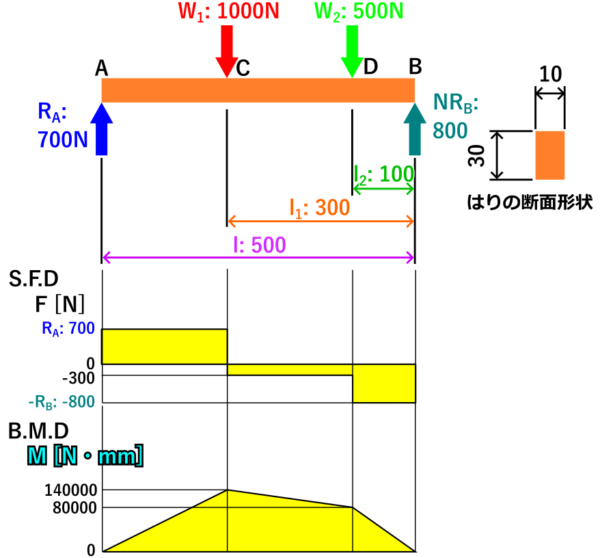
計算したせん断力、曲げモーメントでせん断力図、曲げモーメント図を書いたら次の画像のようになります。
せん断応力、曲げ応力の計算
せん断応力、曲げ応力の計算方法については前回の記事で説明しているので省略しますが、計算結果は下記になります。
せん断応力: 2.67 MPa
最大曲げ応力: 93.3 MPa
材質はSS400なので、引張強さが400 MPa、降伏点が245 MPaとします。
降伏点と最大曲げ応力に着目すると安全率は245 / 93.3 = 2.63。
この安全率で問題なければOKですし、もっと安全率が必要となれば断面積を増やすなどの設計変更が必要となります。
まとめ
複数の荷重がある両端支持ばりの強度は次のステップで計算できます。
① 支点の反力の計算
② せん断力の計算
③ 曲げモーメントの計算
④ せん断応力、曲げ応力を計算して材料の強度と比較して判断
1点集中荷重との違いは、せん断力、曲げモーメント計算時に複数の荷重を合計する点です。

コメント