両端支持ばり(1点集中荷重)が壊れるか壊れないかの強度計算方法
強度を計算するために曲げ応力、曲げモーメント、せん断力、せん断応力、反力を求める必要がありますが、これら計算方法をかつてないほど懇切丁寧に解説したいと思います。
そして、求めた曲げモーメントやせん断力を、どのように強度設計に活かせばいいかも説明します。
教科書では曲げモーメントやせん断力を求めることが目的になってしまいがちですが、実際の設計では本当に知りたいのはそれではなく、荷重により部材が壊れるのか、壊れないか?ですよね。
曲げモーメントやせん断力を求めた上で、部材が壊れるか壊れないかの判断方法についてまでこの記事で説明します。
両端支持ばりの例
そもそも両端支持ばりって何?現実にはどういう状況なの?って思う人もいるかもしれません。
典型的な1点集中荷重の両端支持ばりの例としては、丸太の橋に一人乗ってる状態です。
二人以上乗ってたら荷重が2箇所以上になるので、それについては別の記事で説明したいと思います。
「両端支持ばり」であるためには、丸太の両端は両岸に乗っかっているだけになります。
丸太の両端をコンクリートでガチガチに固めてしまうと、それは「両端固定ばり」になります。
例題
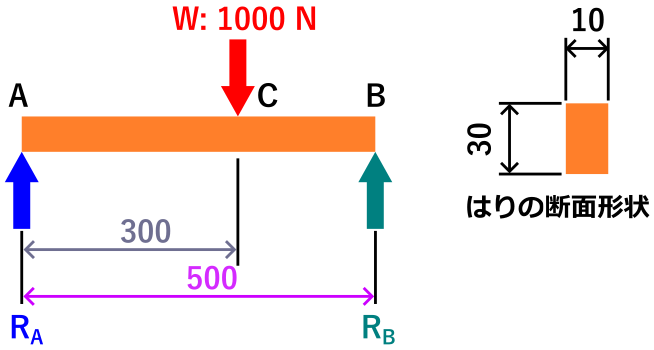
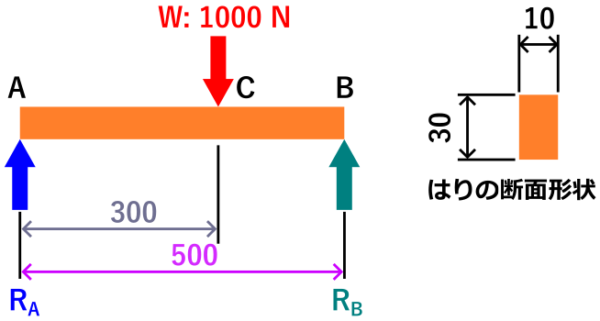
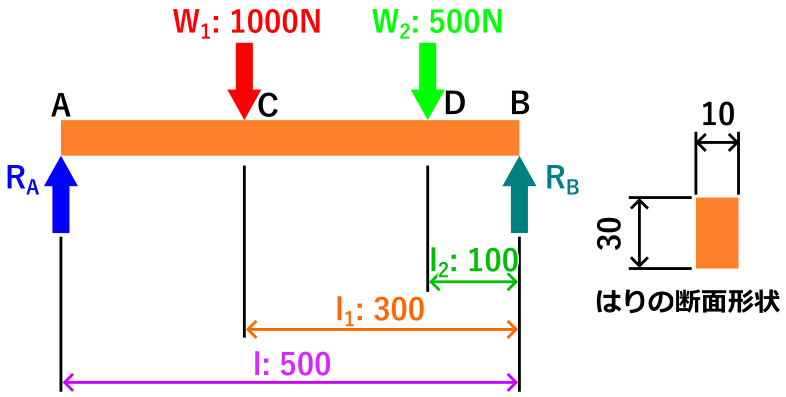
例題として、下の画像のような両端支持ばりがあります。
このはりに作用する反力R_A, R_B、せん断力、最大曲げモーメント、せん断応力、曲げ応力を計算することにします。
そしてこの構造で強度的に問題ないのか?壊れないか?と言うところまで考えたいと思います。
例題を実際に解くのは計算方法の解説の後で。
両端支持ばり強度計算の概要
1点集中荷重の両端支持ばり計算方法の概要です。
詳細は後ほど説明しますが、一度計算方法を理解すれば、この図を見れば思い出せると思います。
①せん断力の計算
①-1 支点の反力の計算
①-2 せん断力の計算、せん断力図の作成
②曲げモーメントの計算
②-1 最大モーメントの計算、曲げモーメント図の作成
③せん断応力、曲げ応力を計算して材料の強度(引張強さ、降伏点)と比較して判断
③-1 せん断応力の計算
③-2 断面係数の計算
③-3 曲げ応力を計算
③-4 せん断応力、曲げ応力を材料の強度(引張強さ、降伏点)と比較して判断
計算方法の詳細
計算方法について詳しく説明します。
はりのつりあい条件について
静止した(外力がつりあった)はりについて、次の条件がなりたちます。
- はりに作用する外力(荷重と反力)の総和は0になる
- 力のモーメントの総和はどの点についても0になる
条件1について、荷重は上からの力、反力は荷重を支えようとする土台の力(はりの自重は考えないことにします)。
荷重と反力がつりあっていないと、はりは静止していられないですよね。
なので、外力の総和は0となります。
条件2についても同様に、はりのモーメント(はりを回転させようとする力)が釣り合っていないと、はりは静止していられません。
そのため、どの点においてもモーメントの総和は0になります。
支点の反力も曲げモーメントもこの条件を満たしているのを前提に計算できるので、「はりのつりあいの条件」は一応覚えておいてください。
外力(荷重、反力)の符号について
つりあいの条件1の「外力(荷重と反力)の総和は0」についてですが、上向きの力を正(+)、下向きの力を負(-)と考えて計算します。
正負の符号は、あくまでここではこうするというだけで、逆にしても問題ありません。
大事なのは、上向きと下向きで符号を変えて考える、ということです。
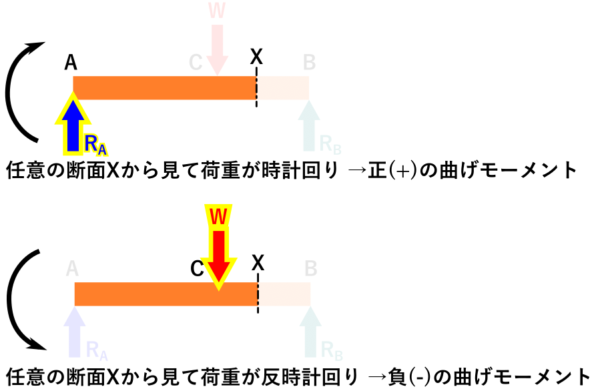
曲げモーメントの符号について
任意の断面の左側で時計回りのモーメントを正(+)、反時計回りのモーメントを負(-)とします。
断面の右側では逆となり、時計回りのモーメントを負(-)、反時計回りのモーメントを正(+)とします。
ややこしいと思ったら、左側だけ考えればOKです。
(正負の符号は、あくまでここではこうするというだけで、逆にしても問題ありません)
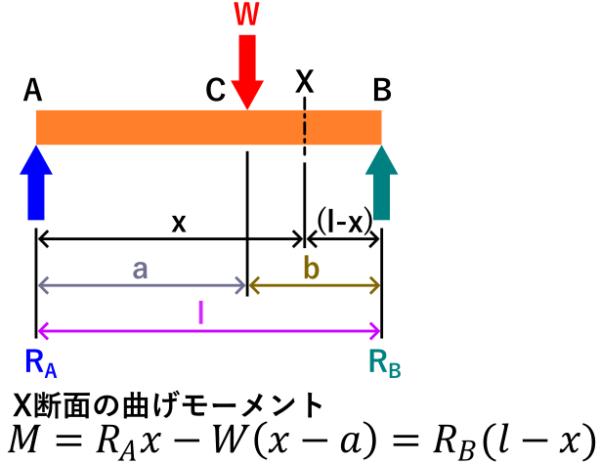
下の例では、曲げモーメントを知りたい断面Xを好きな位置に決めて、その断面Xから見て左側のモーメント「R_A」は時計回りなので正(+)、Wは反時計回りなので負(-)のモーメントとなります。
反力の計算・詳細解説
せん断力や曲げモーメントをこの後計算するんですが、はりを支えようとする「反力」がいくらかを最初に知る必要があります。
反力とは何か?というと、丸太の橋で言うと両岸の地面で受け止める、乗ってる人を支える力になります。
乗ってる人の重量により作用する力が荷重です。
上の画像で言うと「RA」、「RB」が反力です。
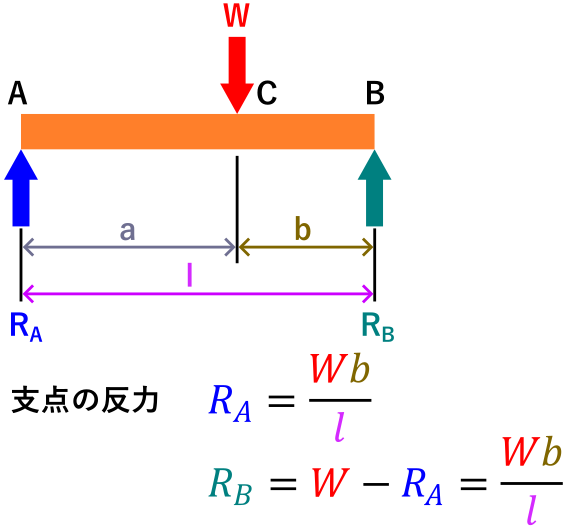
はりに作用している荷重と位置が分かっているとして、はりの釣り合いの条件より反力が求められます。
はりのつりあいの条件1より、外力の総和は0なので、
\[\LARGE R_A+R_B-W=0 \]
| RA | 反力 [N] |
|---|---|
| RB | 反力 [N] |
| W | 荷重 [N] |
はりのつりあいの条件2より、ある点においてのモーメントの総和は0になるので、
\[\LARGE R_Al-Wb=0 \]
| RA | 反力 [N] |
|---|---|
| l | はりの長さ [mm] |
| W | 荷重 [N] |
| b | 荷重の位置 [mm] |
となります。
これは、点Bを中心に考えて、反力R_Aは点Bからの距離がlなのでモーメントはR_A l、点Bから見て時計回りなので符号が正(+)、
荷重Wは点Bからの距離がbなのでモーメントはWb、点B絡みて反時計回りなので符号が負(-)となり、つりあいの条件2より、これらを合計すると0になる、ことを意味しています。
これを変形させると以下の式になり、R_Aが求められます。
反力RAの計算式
\[\LARGE R_A=\frac{Wb}{l} \]
| RA | 反力 [N] |
|---|---|
| W | 荷重 [N] |
| b | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
R_Aが求められたら、つりあいの条件1も使ってR_Bを求めることが出来ます。
反力RBの計算式
\[\LARGE R_B=W-R_A=\frac{Wa}{l} \]
| RB | 反力 [N] |
|---|---|
| W | 荷重 [N] |
| RA | 反力 [N] |
| a | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
せん断力の計算・詳細解説
はりに作用しているせん断力は、場所によって大きさが異なるため、「ここ!」と言う場所(任意の断面)を決めて計算することになります。
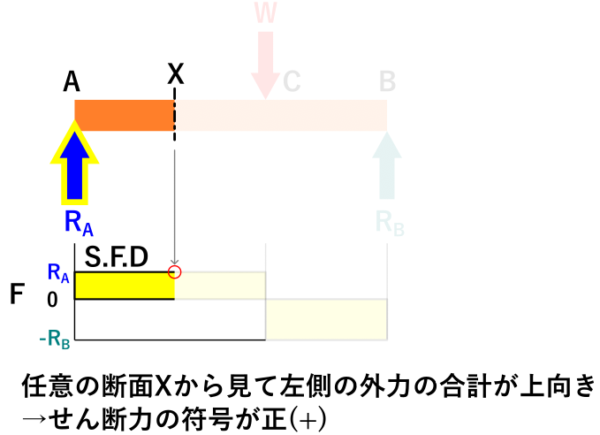
任意の断面から見て左側の、上向きの外力を正(+)、下向きの力を負(-)として合計することで、その断面に作用するせん断力を求められます。
外力の合計が上向きの場合はせん断力の符号が正(+)、下向きの場合は負(-)とします。
(正負の符号は、あくまでここではこうするというだけで、逆にしても問題ありません)
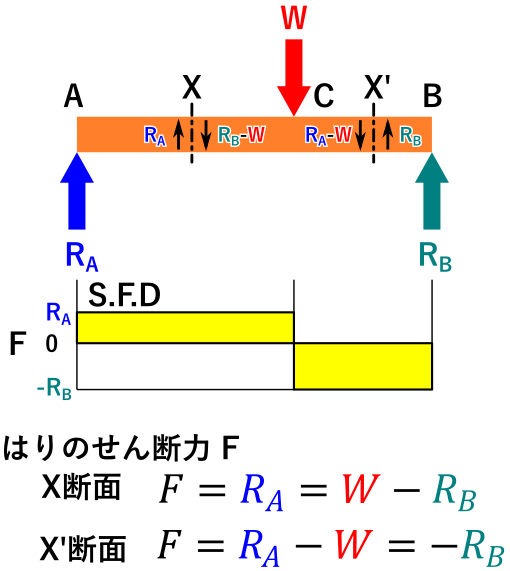
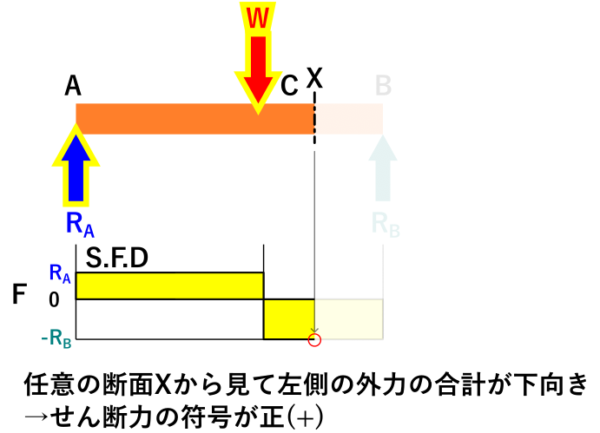
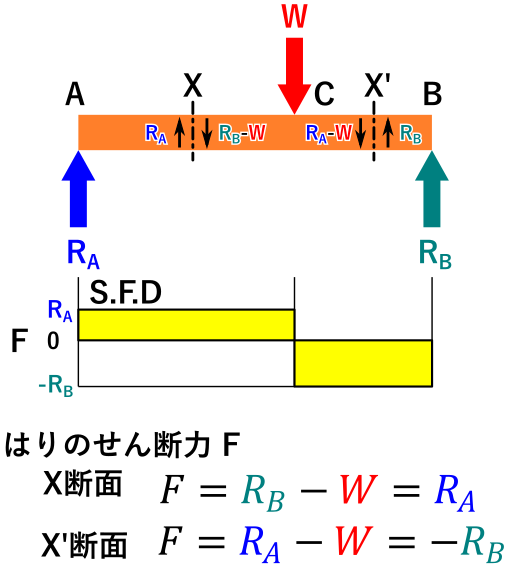
下の画像のX断面に作用するせん断力FはR_A、X’断面のせん断力はRBとなります。
RA、RBは反力としてすでに計算済みなのでその値をそのまま持ってきたらいいだけです。簡単ですね!
ただし、正(+)・負(-)の符号には注意が必要です。
より正確に言うと下の式のように、任意の断面の左側の上向きの外力(荷重や反力)に正(+)、下向きの外力に負(-)の符号をつけて合計したものが、その任意断面に作用するせん断力となります。(または右側の外力の符号を逆にして合計しても同じことです。)
X断面のせん断力の計算式
\[\LARGE F=R_A=W-R_B \]
X’断面のせん断力の計算式
\[\LARGE F=R_A-W=-R_B \]
| F | せん断力 [N] |
|---|---|
| RA | 反力 [N] |
| RB | 反力 [N] |
| W | 荷重 [N] |
黄色いグラフみたいなやつは「せん断力図(S.F.D)」と言い、はりのどの場所にどれだけのせん断力を受けているのかを示したものです。
各断面についてせん断力を計算し、線でつなぐことで描くことが出来ます。
見てのとおり両端支持の1点集中荷重の場合は、荷重Wの位置でせん断力が正(+)から負(-)に反転します。
この後説明しますが、この場所で曲げモーメントが最大となり、「危険断面」と呼びます。
曲げモーメントの計算・詳細解説
曲げモーメントについてもせん断力と同じく、はりの場所によって作用している曲げモーメントの大きさが異なります。
なので、「ここ!」と言う場所(任意の断面)を決めて曲げモーメントを計算します。
モーメントの計算は、外力の大きさと外力までの距離を掛け算すれば求められます。
さっきも説明しましたが、ここでは断面の左側で時計回りのモーメントを正(+)、反時計回りのモーメントを負(-)とします。
下の図の任意断面Xの曲げモーメントの計算方法としては、はりのつりあいの条件2より、ある点においてのモーメントの総和は0になるのでとりあえず任意断面Xの左側のモーメントだけ考えればOK。
各外力(RA, W)のモーメントを求め、時計回りのモーメントのRAは正(+)の符号、Wは負(-)の符号を付けて合計すると、任意断面Xの曲げモーメントが計算できます。
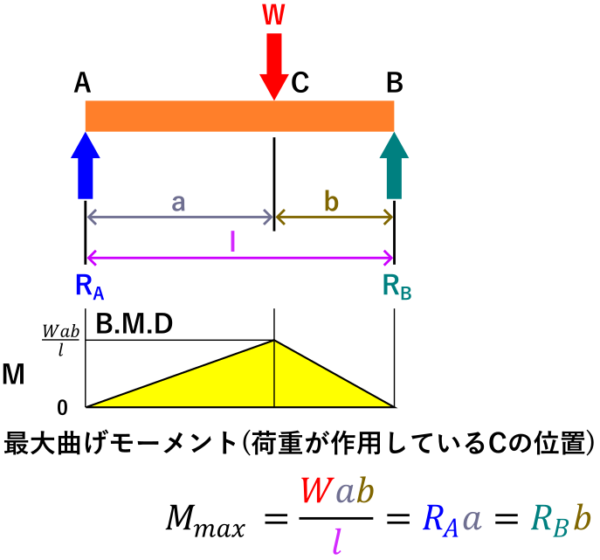
各断面について曲げモーメントを計算すると、下の図の黄色いグラフみたいな「曲げモーメント図 (B.M.D)を描くことができます。
曲げモーメント図を見ると、荷重Wの位置に最大曲げモーメントが作用しています。
下のせん断力図で、せん断力の符号が正(+)から負(-)に反転していますが、ここに最大曲げモーメントが作用し、「危険断面」と呼びます。
はりの強度を計算したい時、最大曲げモーメントがいくらか?というのが重要になってくるので、曲げモーメントについては最大曲げモーメントのみ計算すればよいでしょう。
両端支持ばり(1点集中荷重)の最大曲げモーメントの計算式
\[\LARGE M_{max}=\frac{Wab}{l}=R_Aa=R_Bb \]
| Mmax | 最大曲げモーメント [N・mm] |
|---|---|
| RB | 反力 [N] |
| W | 荷重 [N] |
| a | 荷重の位置 [mm] |
| b | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
| RA | 反力 [N] |
| RB | 反力 [N] |
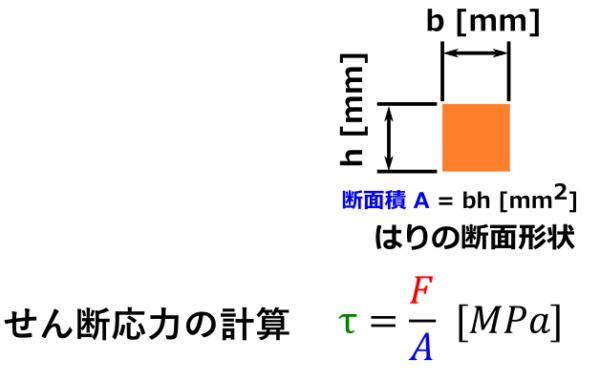
せん断応力の計算
せん断応力とは、部材にせん断力が加えられたときに材料内部に生じる内力のこと。
せん断力の計算でははりの断面積とせん断力は無関係でしたが、せん断応力は断面積によって大きさが変わります。
同じせん断力を断面積が大きい部材で受けるのと、小さい部材で受けるのでは発生する応力が異なり、小さいほうが応力が大きくなる = 壊れやすいと考えることが出来ます。
せん断応力のさらに詳しい計算方法についてはこちらの記事で説明しています。
せん断応力の計算式はこちら。
せん断力を断面積で割ると、せん断応力が求められます。
せん断応力の計算式
\[\LARGE \tau=\frac{W}{A} \]
| τ(タウ) | せん断応力 [MPa] |
|---|---|
| F | せん断力 [N] |
| A | 断面積 [mm2] |
曲げ応力の計算
次に曲げ応力を求めますが、曲げ応力を求めるためには曲げモーメントと断面係数の情報が必要になります。
なので、まずは部材の断面係数を計算します。
断面係数の計算
断面係数とは、はりの断面形状によって決まる値です。
数値が大きいほど曲げモーメントに対して強いはりと言えます。
つまり曲げ応力が小さくなります。
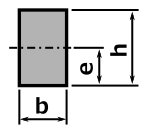
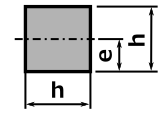
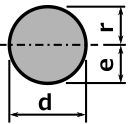
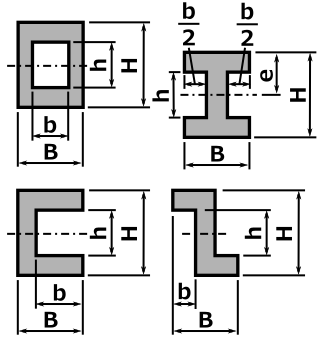
下記の表に、各形状の断面形状の計算方法ついて記します。
|
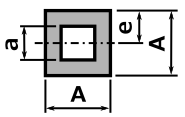
断面 |
断面積 A |
重心の距離 e |
断面二次モーメント I |
断面係数 Z = I / e |
 |
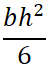 |
|||
 |
||||
 |
 |
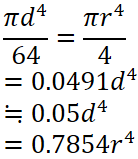 |
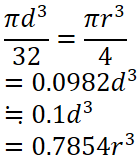 |
|
 |
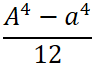 |
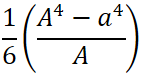 |
||
 |
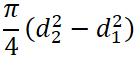 |
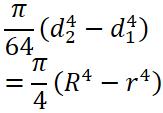 |
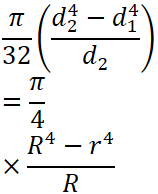 |
|
 |
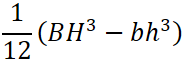 |
 |
曲げ応力の計算
曲げモーメントと断面係数を計算済みであれば、曲げ応力は簡単に求められます。
曲げモーメントを断面係数で割ることで曲げ応力を求められます。
曲げ応力の計算式
\[\LARGE \sigma_b=\frac{M}{Z} \]
| σb | 曲げ応力 [MPa] |
|---|---|
| M | 曲げモーメント [N・mm] |
| Z | 断面係数 [mm3] |
せん断応力、曲げ応力を材料の強度(引張強さ、降伏点)と比較して判断
せん断応力、曲げ応力の計算方法を今までの説明でしましたが、これをどうやって設計に活かせばよいのでしょうか?
せん断応力、曲げ応力が、部材の持つ強さ(引張強さや降伏点)を超えれば破断や永久ひずみが残る、と言うふうに判断します。
よく使われる鉄系材料のSS400ですが、記号が表す「400」が引張強さを表し、「400 MPa」の引張強さを保証しています。
計算した曲げ応力が400 MPaを超えている場合、曲げにより破断する可能性があります。
「曲げ応力」は部材の内部では「引張応力」と「圧縮応力」が発生した状態なので、材料の「引張強さ」や引張の降伏点と比較して判断します。
せん断力についても、材料のせん断強さなどと比較して判断しますが、注意が必要なのは、材料のせん断強さは引張強さより小さく、約0.6倍程度になります。
SS400の場合、400 × 0.6 = 240 [MPa]以上のせん断力により破断する可能性があります。
主な材料の強さを下表にまとめました。
※あくまで目安です。この数値が正しい保証はないのでしっかり調べてから設計してくださいね。
| 種類 | 記号 | 降伏点または耐力 N/mm2 (= MPa) | 引張強さ N/mm2 (= MPa) | 降伏せん断強さN/mm2 (= MPa) | 極限せん断強さN/mm2 (= MPa) |
|---|---|---|---|---|---|
| 一般構造用圧延鋼 | SS400 | 245 | 400~510 | 147 | 240~306 |
| 機械構造用炭素鋼 | S45C | 345 | 570 | 207 | 342 |
| 機械構造用合金鋼 | SCM435 | 785以上 | 930以上 | 471以上 | 558以上 |
| ステンレス | SUS304 | 205 | 520 | 123 | 312 |
| ステンレス | SUS430 | 205 | 420 | 123 | 252 |
| アルミ合金 | A5052(質別: O) | 65 | 170~215 | 39 | 102~129 |
| アルミ合金(超々ジュラルミン) | A7075(質別: T6) | 240~460 | 360~545 | 144~276 | 216~327 |
| タフピッチ銅 | C1100(質別: O) | 69以上 | 195以上 | 41.4以上 | 117以上 |
| 黄銅 | C2801 | – | 325~470以上 | – | 195~282以上 |
せん断応力、曲げ応力が材料の強さよりも小さくても、ギリギリだったら危険です。
想定外の荷重によりすぐに壊れてしまってはいけませんからね。
このような想定外の荷重や材料の欠陥、経年変化等を見越して余裕を持たせておくために「安全率」を設定します。
この話は長くなるので、下記の記事を参考にしてください。
例題の計算
反力の計算
まず反力RAを計算してみましょう。
反力RAの計算式
\[\LARGE R_A=\frac{Wb}{l} \]
| RA | 反力 [N] |
|---|---|
| W | 荷重 [N] |
| b | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
式に、例題から読み取った下記の値を代入して計算すると反力RAは400 Nとなります。
\[\LARGE\begin{eqnarray} R_A&=&\frac{1000\times(500-300)}{500}\\ &=&400[N] \end{eqnarray}\]
| W | 1000 [N] |
|---|---|
| b (=l-a) | 500-300 [mm] |
| l | 500 [mm] |
次は反力RBの計算。
反力RBの計算式
\[\LARGE R_B=W-R_A=\frac{Wa}{l} \]
| RB | 反力 [N] |
|---|---|
| W | 荷重 [N] |
| RA | 反力 [N] |
| a | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
RBを求めるには\(W-R_A\)でも\(\frac{Wa}{l}\)でもどちらを使っても構いませんが、\(W-R_A\)の式で計算してみましょうか。
下記の計算の結果、反力RBは600 Nとなりました。
\[\LARGE\begin{eqnarray} R_B&=&1000−400\\&=&600[N]
\end{eqnarray}\]
| W | 1000 [N] |
|---|---|
| RA | 400 [N] |
せん断力の計算
\[\LARGE F=R_B-W=R_A \]X’断面のせん断力の計算式
\[\LARGE F=R_A-W=-R_B \]
| F | せん断力 [N] |
|---|---|
| RA | 反力 [N] |
| RB | 反力 [N] |
| W | 荷重 [N] |
はりに作用するせん断力は、一点集中荷重の両端支持ばりの場合は、反力RA, RBの値をそのまま持ってきたらいいだけでしたね。
X断面のせん断力は400 Nになります。
X’断面のせん断力は-600 Nになります。(符号に注意)
最大曲げモーメントの計算
両端支持ばり(1点集中荷重)の最大曲げモーメントの計算式
\[\LARGE M_{max}=\frac{Wab}{l}=R_Aa=R_Bb \]
| Mmax | 最大曲げモーメント [N・mm] |
|---|---|
| RB | 反力 [N] |
| W | 荷重 [N] |
| a | 荷重の位置 [mm] |
| b | 荷重の位置 [mm] |
| l | はりの長さ [mm] |
| RA | 反力 [N] |
| RB | 反力 [N] |
最大曲げモーメントを求める計算は上の通り何種類かあり、どれを使っても同じです。
反力をすでに求めているので、以下の計算でやってみると、最大曲げモーメントは120000 N・mmとなりました。
\[\LARGE M_{max}=R_Aa\\=400\times300\\=120000N・mm\]
| RA | 400 [N] |
|---|---|
| a | 300 [mm] |
せん断応力の計算
せん断応力の計算式
\[\LARGE \tau=\frac{F}{A} \]
| τ(タウ) | せん断応力 [MPa] |
|---|
せん断力を部材の断面積で割るとせん断応力が求められます。
せん断力は先程計算済みですが、断面積の計算がまだですね。
例題よりはりの断面は幅10 mm、高さ30mmなので、
\[\LARGE 10×30=300[mm^2] \]
となります。
断面形状は一様なので、X断面よりもせん断力の大きいX’断面のほうが心配です。
X’断面についてせん断応力を計算してみると、せん断応力は2 MPaとなりました。
\[\LARGE\begin{eqnarray} \tau&=&\frac{600}{300}\\ &=&2[MPa] \end{eqnarray}\]
| F | 600 [N] |
|---|---|
| A | 300 [mm2] |
曲げ応力の計算
曲げ応力の計算は下の図のように、まずは断面係数を求める必要があります。
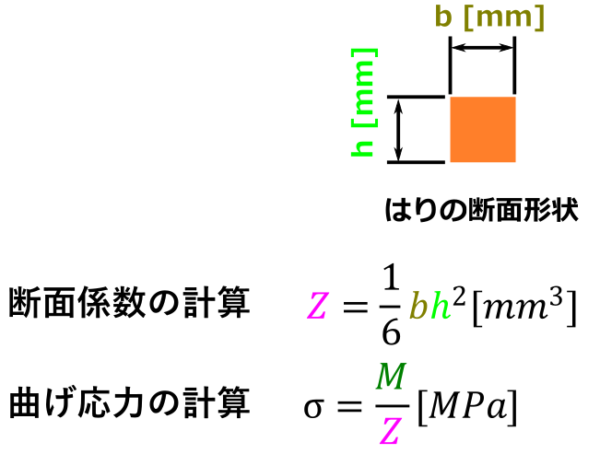
断面係数の計算
今回計算するはりは長方形断面なので、断面係数の計算式は下記になります。
\[\LARGE Z=\frac{bh^2}{6} \]
| Z | 断面係数 [mm3] |
|---|---|
| b | はりの幅 [mm] |
| h | はりの高さ [mm] |
例題から読み取った寸法を代入して計算すると、断面係数は1500 mm3となりました。
\[\LARGE\begin{eqnarray} Z&=&\frac{1}{6}\times{10\times30}^2\\ &=&1500[mm^3] \end{eqnarray}\]
| b | 10 [mm] |
|---|---|
| h | 30 [mm] |
曲げ応力の計算
最大曲げモーメントと断面係数がわかったので、曲げ応力が計算できます。
\[\LARGE \sigma_b=\frac{M}{Z} \]
| σb | 曲げ応力 [MPa] |
|---|---|
| M | 曲げモーメント [N・mm] |
| Z | 断面係数 [mm3] |
計算式に、計算済みの最大曲げモーメントと断面係数を代入して計算すると、このはりに発生する最大曲げ応力は80 MPaとなりました!
\[\LARGE\begin{eqnarray} \sigma_b&=&\frac{120000}{1500}\\ &=&80[MPa] \end{eqnarray}\]
| M | 120000 [N・mm] |
|---|---|
| Z | 1500 [mm3] |
せん断応力、曲げ応力の値を判断する
計算の結果、せん断応力、最大曲げ応力は下記の値となりました。
これをどう判断するかが非常に重要です。
| せん断応力 | 2 [MPa] |
|---|---|
| 最大曲げ応力 | 80 [MPa] |
材質はSS400と言う想定なので
- 引張強さ 400 MPa
- 降伏点 245 MPa
程度となります。
400 MPa以上の応力が生じるとちぎれるし、245 MPa以上の応力でもとに戻らない永久変形が起こると考えられます。
これに対してせん断応力 2 MPaはかなり余裕があるので、問題ないと考えて良いでしょう。
最大曲げ応力 80 MPaは、降伏点の約1/3、つまり降伏点に対する安全率が約3となります。
安全率3で問題ないのか?というのに明確な答えはなく設計者の判断、または業界等のルールによります。
静的な荷重であれば特に問題ないけど、繰返し荷重だったら少し心もとない、みたいな判断になります。
許容応力や安全率の考え方については下記の記事でもまとめているので参考にしてください。
まとめ
説明がやたら長くなってしまいましたが(記事を分ければよかったかも)、1点集中荷重の両端支持ばりの強度計算方法はだいたいこれでOKじゃないでしょうか?
両端支持ばりの荷重が複数ある場合も、同じような方法で計算可能なので、需要があればそのうち書いてみようかと思います。

コメント