軸にねじる力を加えると、当然ねじれるように変形するわけですが、具体的に何rad、何度変形するのでしょうか?
単純な丸棒やパイプであれば、それ計算で求められます。
軸をねじった時の変形量の計算方法を例題を交えながら説明したいと思います。
この記事を読めば丸棒(中実円断面)やパイプ(中空円断面)の変形量(ねじれ角)を手計算出来るようになります。
軸をねじった時に発生する応力や、長方形・正方形断面の応力、ねじれ角の計算方法については下記の記事で説明しています。
この記事の目次
ねじれ角計算の例題
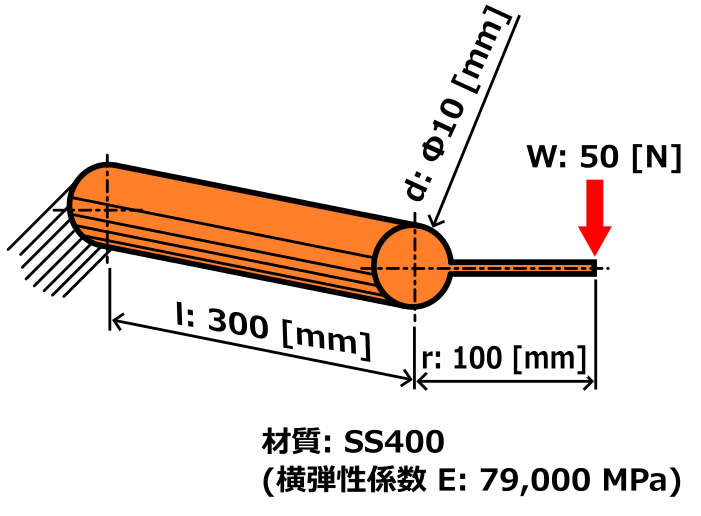
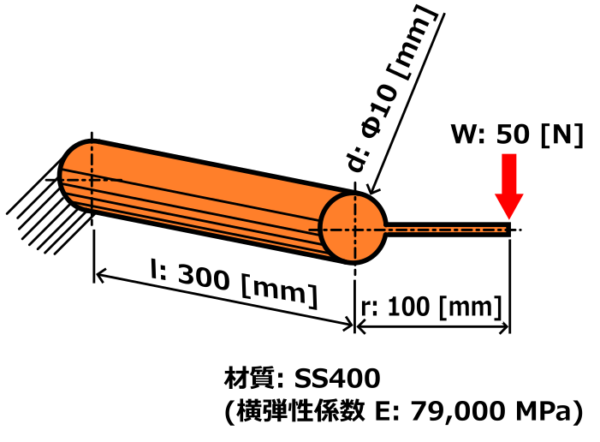
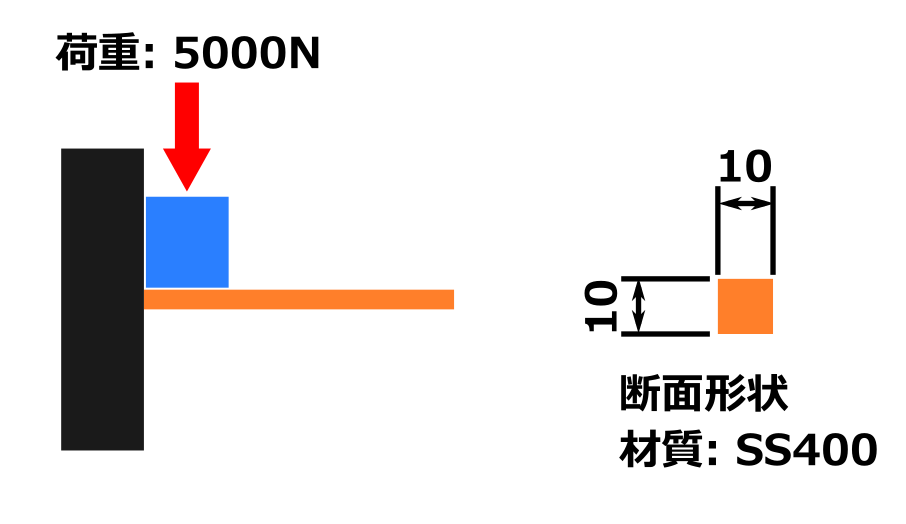
下の画像の状況の時、軸のねじれ角はいくらになるでしょうか?
書き出してみると、下記のような条件となります。
- 軸の直径 10 mm
- ねじりモーメント 5000 N・mm (中心から100 mmの位置に50 N)
- 材質 : SS400 (横弾性係数 79000 MPa)
- 軸の長さ 300 mm
※ 曲げ応力は発生せず、ねじり応力のみ発生するものとします。
計算方法の説明をしつつ、この例題を解いていきたいと思います。
ねじれ角計算の概要
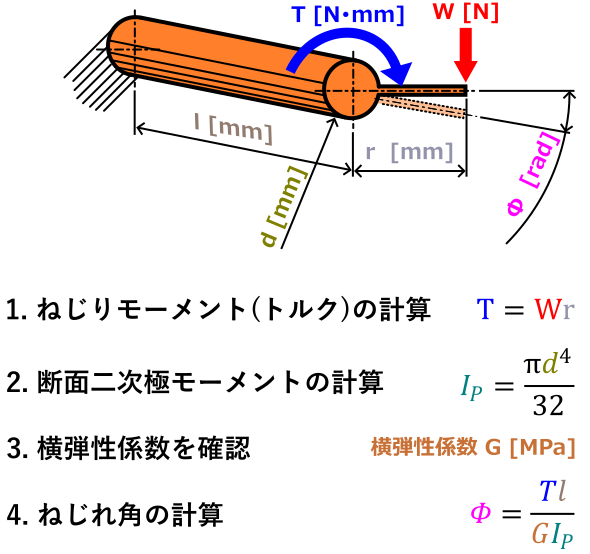
計算方法を詳しく見ていく前に、ねじれ角の計算方法の全体像です。
次の手順でねじれ角を計算することが出来ます。
- ねじりモーメント(トルク)の計算
- 断面二次極モーメントの計算
- 横弾性係数を確認
- ねじれ角の計算
※上の画像の式は中実円断面(中身の詰まった丸棒)の場合です。中空円断面(パイプ)の場合は少し式が異なります。
| T | ねじりモーメント(トルク) [N・mm] |
|---|---|
| r | 中心から荷重の距離 [mm] |
| W | 荷重 [N] |
| IP | 断面二次極モーメント [mm4] |
| π(パイ) | 円周率 |
| d | 軸の直径 [mm] |
| G | 横弾性係数 [MPa] |
| l (小文字のエル) | 軸の長さ [mm] |
| Φ (ファイ) | ねじれ角 [rad] |
[mntyzer_topmedium]
ねじれ角の計算方法詳細
では計算方法を見ていきましょう。
計算方法の説明 → 例題を計算と言う順序で1ステップずつ説明します。
ねじりモーメント(トルク)の計算
まずは軸に加えられるねじりモーメント(トルク)の計算。
トルクがすでに分かっている場合はもちろん計算する必要はありません。
荷重と、中心からの距離を掛け算するとトルクが求められます。
ねじりモーメント(トルク)の計算式
\[ T=Wr\ [N・mm] \]
| T | ねじりモーメント(トルク) [N・mm] |
|---|---|
| r | 中心から荷重の距離 [mm] |
| W | 荷重 [N] |
例題の計算
例題をのねじりモーメント(トルク)を計算してみましょう。
式に代入するパラメータは、例題の図より下記になります。
| r | 100 [mm] |
|---|---|
| W | 50 [N] |
式に代入して計算すると、トルクは5,000 N・mmとなりました。
\[\begin{eqnarray} T&=& 50\times100\\ &=& 5000\ [N・mm] \end{eqnarray}\]
断面二次極モーメントの計算
続いて断面二次極モーメントの計算。
断面二次極モーメントの値が大きいほど、その断面形状はねじりに対して変形しにくいことを表します。
材質には関係なく、形状とサイズのみによって決まる値です。
中実円断面と中空円断面の断面二次極モーメントの計算式を下記に示します。
中空円断面の断面二次極モーメントの式
\[
I_P=\frac{\pi}{32}(d_2^4-d_1^4)
\]
| IP | 断面二次極モーメント [mm4] |
|---|---|
| π(パイ) | 円周率 |
| d2 | 軸の外形 [mm] |
| d1 | 軸の内径 [mm] |
例題の計算
今回は例題は断面形状が中身の詰まった中実円なので、中実円断面の式を使って断面二次極モーメントを計算します。
代入するパラメータはこちら。
| d | 10 [mm] |
|---|
値を代入して計算すると、981.75 mm4となりました。
$$\begin{eqnarray}
I_P&=&\frac{\pi\times10^4}{32}\\
&=&981.75\ [mm^4]
\end{eqnarray}$$
横弾性係数を確認
横弾性係数とは、材料にせん断荷重が加えられた時の変形の度合いを表す数値です。
数値が大きいほどせん断やねじりに対して変形しにくい材料となります。
下表にいくつかの材料の横弾性係数を下記に示しますので、参考にしてください。
※熱処理条件等により数値が大きく変動することがあります。正確な値は規格等で確認してください。
※樹脂材料の縦弾性係数は引張弾性率を記載
※樹脂材料の横弾性係数は縦弾性係数の40%とした場合の目安
| 材質 | 横弾性係数 G [MPa (N/mm2)] |
|---|---|
| 軟鋼(SS400) | 79,000 |
| 鋼(SCM435) | 83,000 |
| ステンレス(SUS304) | 74,000 |
| リン青銅(C5191) | 40,000 |
| アルミニウム(A5052) | 26,000 |
| 銅(C1100) | 44,000 |
| 樹脂(ABS) | 1,220 |
| 樹脂(PP) | 600 |
| 樹脂(PE) | 400 |
| 樹脂(PMMA) | 1,320 |
| 樹脂(POM) | 940 |
| 樹脂(PC) | 960 |
| 樹脂(PA66) | 1,200 |
例題の計算
材質がSS400なので上の表より横弾性係数は79,000 MPaとなります。
ねじれ角の計算
必要な値が揃ったので、いよいよねじれ角の計算です。
ねじれ角の計算式はこちら。
ねじれ角の式
$$
\Phi=\frac{Tl}{GI_P}
$$
| Φ (ファイ) | ねじれ角 [rad] |
|---|---|
| T | ねじりモーメント(トルク) [N・mm] |
| l (小文字のエル) | 軸の長さ [mm] |
| G | 横弾性係数 [MPa] |
| IP | 断面二次極モーメント [mm4] |
計算結果の値はラジアンなので、必要があれば次の式で度に換算しましょう。
\[ 度=rad\times\frac{180}{\pi} \]
ちなみに、今回説明しているねじれ角の計算式ですが、残念ながら断面が円形以外の場合は使えません。
長方形の断面二次極モーメントを計算してこの式に代入してもダメってことです。(長方形断面のねじれ角は下記の記事で説明しています)
例題の計算
例題を計算します。
代入するパラメータは下記。
| T | 5000 [N・mm] |
|---|---|
| l (小文字のエル) | 300 [mm] |
| G | 79000 [MPa] |
| IP | 981.75 [mm4] |
計算すると、下記の通りねじれ角は0.0193 radとなりました!
\[\begin{eqnarray} \Phi&=&\frac{5000\times300}{79000\times981.75}\\ &=&0.0193\ \left[rad\right] \end{eqnarray}\]
単位を「度」に換算すると、以下の計算の通り1.11度のねじり角となります。
\[ 0.0193\times\frac{180}{\pi}=1.11\ [°] \]
計算式の分子に軸の長さlが入っていることから分かるように、ねじり角は軸の長さに比例します。
今回の例だと、軸の長さが100 mあれば同じ力を加えれば1回転する計算になりますね。
比ねじれ角を基準に軸の直径を決定する方法
ねじれ角の計算方法は以上ですが、少し話が変わって機械設計において軸の直径を決定する時、下記の2つの選択肢があります。
- 軸に発生するねじり応力を基準にする
- 比ねじれ角を基準にする
軸に発生するねじり応力を基準にする場合は、材料の降伏せん断応力などに適当な安全率を設定して許容応力を決定します。
発生する応力が許容応力以下になればOK、と言う考え方です。
ねじり応力の計算方法は下記の記事で説明しています。
一方、比ねじれ角を基準にする場合、手元の文献では「比ねじれ角は1/4 ~ 1/16 [度/m]くらいにとり、回転数Nが大きいほど小さい値にとります。一般の伝動軸の場合、許容比ねじれ角は1/4 [度/m]を限度にするのが標準です。」とあります。
文面から、モーターなどの動力を伝える軸について書かれた内容ですが、一つの参考にして良いと思います。
比ねじれ角とは、1mあたりのねじれ角を表すため、先程計算したねじれ角を軸の長さ [m]で割ればOKです。
(上の説明は「1/4 ~ 1/16 度/m」と書いてますが、下の計算は「rad/m」となっていて単位が異なるので注意です)
比ねじれ角の式
\[ \theta=\frac{\mathrm{\Phi}}{l}[rad/m] \]
| θ (シータ) | 比ねじれ角 [rad/m] |
|---|---|
| Φ (ファイ) | ねじれ角 [rad] |
| l (小文字のエル) | 軸の長さ [m] |
単位を「rad/m」から「度/m」への換算は下記計算で出来ます。
\[ 度/m=rad/m\times\frac{180}{\pi} \]
今回の例題では、ねじれ角が0.0193 rad、軸の長さが300 mm = 0.3 mなので被ねじれ角を計算すると、
\[\begin{eqnarray} \theta&=&\frac{0.0193}{0.3}\\ &=&0.0645 [rad/m] \end{eqnarray}\]
となり、「度/m」に換算すると、
\[ 0.0645\times\frac{180}{\pi}=3.69 [度/m] \]
となります。
「一般伝動軸は1/4 [度/m] (0.25 [度/m])以下」と言う基準に当てはめると、大きく超えているため、このサイズでは使用不可となります。
この例で比ねじれ角を0.25 度/m以下にすると、発生するせん断応力は1.7 MPa程度とかなり小さい値になりました。
材質を仮にSS400とすると、降伏せん断応力は140 MPa前後なので、安全率は80倍以上!
伝動軸について言及した内容なので、繰り返し応力がかかる前提で、安全率を大きめに取っていると考えることも出来ます。
繰り返し応力のかからない構造材であれば、0.25 度/mと言わず、もっと攻めても大丈夫でしょう。
まとめ
中実円、中空円断面の軸のねじれ角は次の手順で計算することが出来ます。
- ねじりモーメント(トルク)の計算
- 断面二次極モーメントの計算
- 横弾性係数を確認
- ねじれ角の計算


コメント