【ボルトの強度】軸力に外力(引張)は加算されるのか？

ボルト(ねじ)に適当なトルクを加えて締め付けると、軸力が発生します。
軸力とはボルトが引っ張られる力で、被締結物を固定する力となります。
一方、ボルトを一定以上の力で引っ張ると破断してしまいます。

まてよ？軸力により最初からボルトが引っ張られた状態にあり、さらに外力により引っ張られると、軸力と外力が加算されてしまう！？
そうなると、ボルトの強度がとっても心配！

そんなお悩みのあなたのために、この問題をきっぱりと解決したいと思います。

結論: 軸力と外力は加算されない

最初に結論を書いておきますが、軸力と外力は加算されません。
ご安心ください。

実験してみたら分かると思いますが、なかなか出来ないので頭の中でシミュレートしてみます。

あるところにこんなM3ネジがありました。

• 強度区分 4.6
• T系列 標準締め付けトルク 0.63 N・mで締め付ける
• その時の標準軸力 1050 N
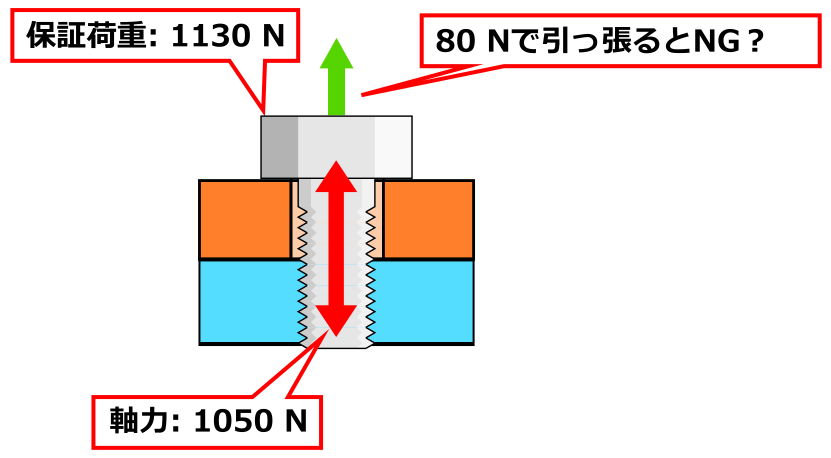
• ボルトの保証荷重 1130 N (JIS B1051)
• 最小極限引張力 2010 N (JIS B1051)

締め付けトルクの値とかは今回はどうでも良くて、とにかく初期状態で1050 Nの軸力でボルトが引っ張られていると思ってください。
そして保証荷重が1130 N。
1130 N以上の引張力がボルトにかかったら、とにかくNGと思ってください。

保証荷重 1130 [N] – 標準軸力 1050 [N] = 80 [N]

え？初期状態からたったの80 N加えたただけで保証荷重をオーバーしちゃうの？
困るなあ・・・

もちろん、そんなことはありません！
初期軸力1050 Nがすでにボルトにかかっていても、保証荷重の1130 Nの荷重を加えることが出来ます。

(安全率とか考慮したら、M3ボルト1本に1130 Nの荷重なんて正気の沙汰じゃねえ！って感じですが、ここでそういう議論はしません)

ボルトと被締結部材はバネである

ボルトの締結で大事な考え方ですが、「ボルトや、ボルトで締結される部材はバネである。」ということ。
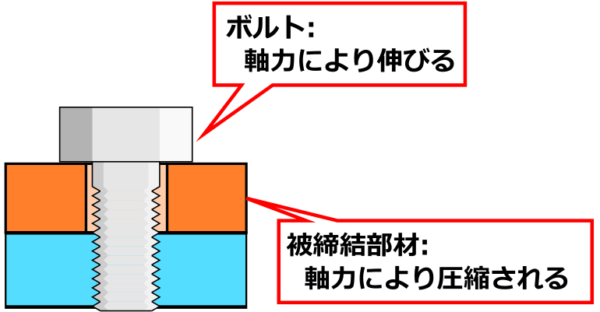
ちょっと何言ってるか分からないかもしれませんが、カッチカチの鉄で出来たボルトも、引っ張ったらわずかに伸びるんです。
ボルトで締結される部材もボルトで締め付けられたら縮むのです。

このわずかに伸びたり縮んだりした物体は力を取り除くと元の寸法に戻るのですが、その元に戻ろうとする反発力が軸力を生み出します。

初期状態では軸力1050 Nが加わった状態 → 引っ張られて伸びたボルトが縮もうとする力と被締結部材が圧縮されてもとに戻ろうとする力が軸力となる。
ボルトと被締結部材がもとに戻ろうとする力は釣り合っているため同じです。

軸力のかかったボルトの頭を引っ張ると？

先程のM3ボルトの頭を引っ張ってみましょう。

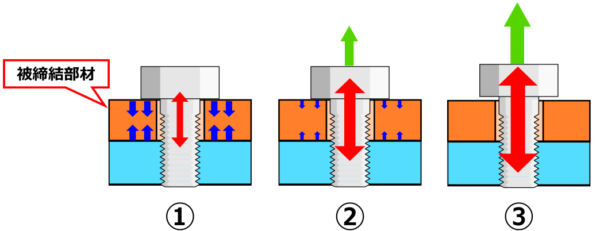
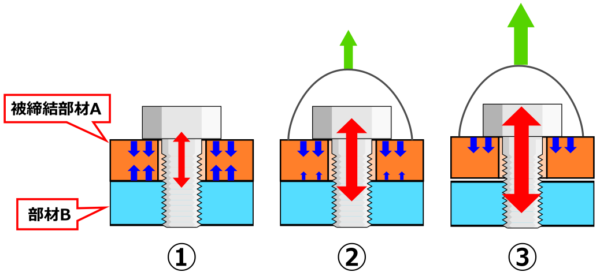
まず、ボルトが締め付けられて頭を引っ張ってない状態。(上図①)
ボルトの頭を引っ張ると、ボルトがさらに伸びますよね。
と同時に、ボルトが伸びた分、被締結部材の圧縮量が減るため、被締結部材の反発力が減少。(上図②)

さらに引っ張ってボルトを伸ばすと、被締結部材の圧縮が0になる、つまり被締結部材は固定されてなくてスカスカのフリー状態に。(上図③)
この時ボルトに加わっている荷重は外力による引張力のみとなり、被締結部材から受ける反発力は0です。
つまり、初期軸力と外力は加算されないってことです。

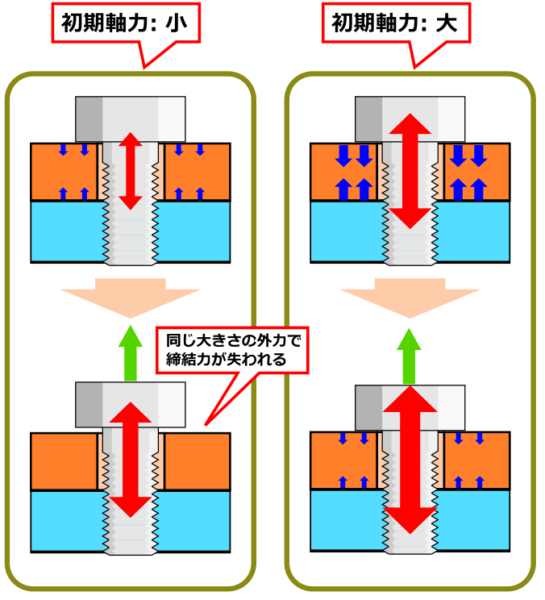
初期軸力の大小はどう影響するかというと、

• 初期軸力が小さい → 被締結部材の圧縮が0になるタイミングが早くなる
• 初期軸力が大きい → 被締結部材の圧縮が0になるタイミングが遅くなる

となるだけで、ボルト引っ張られて破断する時点では初期軸力の大小は関係なくなります。

もちろん、初期軸力がどうでもいいわけではありません。
被締結部材の圧縮が0になった時点で、締結の役目を果たしていないことになります。
外力に対して、部材がきちんと締結された状態を保つためには適切な初期軸力が必要です。

被締結部材を引っ張る場合は？

ボルトの頭を引っ張る場合はわかったけど、被締結部材が引っ張られた場合は？
初期軸力に荷重が加算されるんじゃないの？って疑り深い人なら思いますよね。

いいえ、されません。
ボルトの頭を引っ張るときと同じです。

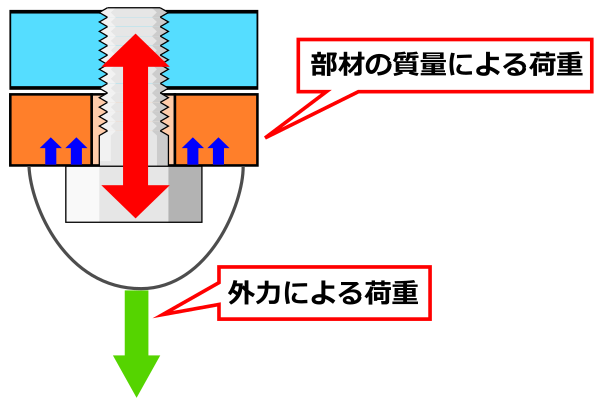
この時の引張の外力は、めねじが加工されている部材Bと被締結部材Aの間で生じている圧縮力を弱めるように作用します。(上画像②)
さらに引っ張ると部材Bと被締結部材Aの間は接触せず浮いた状態となり、A, B間の圧縮力は0となります。(上画像③)
この時ボルトに加わっている荷重は引張の外力のみとなり、やはり初期軸力は関係なくなります。

仮に部材が吊り下げられている場合は、ボルトが破断するかに影響するのは部材の重量による荷重 + 想定される引張力(外力)となり、初期の軸力は関係ありません。

引っ張りバネのモデルで説明

なんかしっくりこないという人のために視点を変えて、違う例えで説明してみます。
え？くどいですか？

さっきボルトはバネだと説明しましたが、ボルトをバネそのものに例えてみましょう。
引っ張りバネを応用したバネ秤(ばかり)と言うものがありますが、一定の荷重で一定の量伸びます。
目盛りが振ってあって、伸びた量を荷重として読み取れるしくみです。

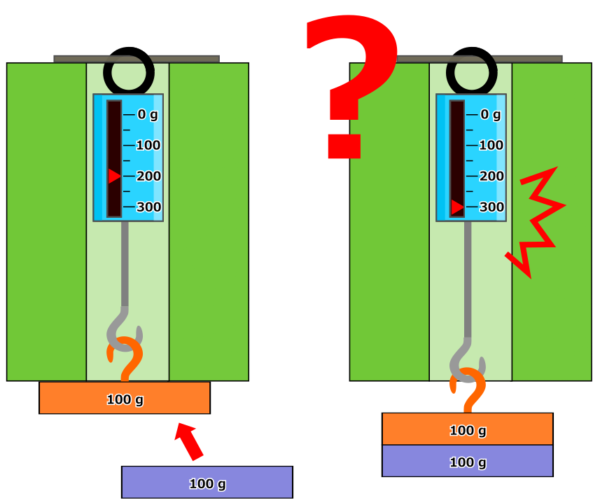
この例えではバネ秤がボルトに相当し、次の条件を想定します。

• バネ秤が300 gで壊れるとする。→ ボルトの保証荷重や引張強度に相当
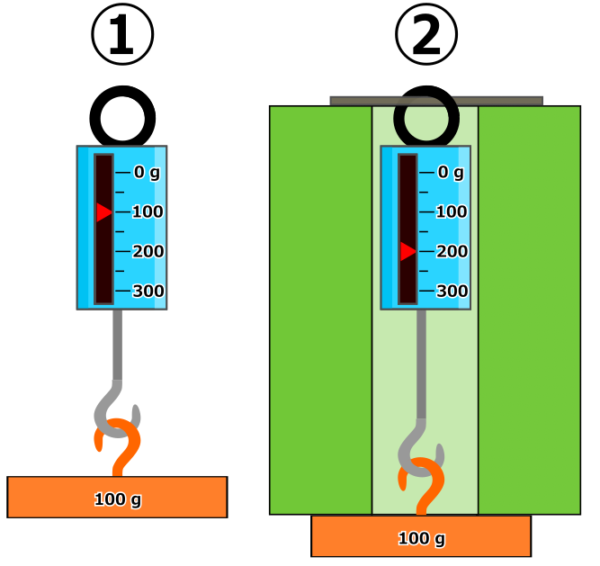
• おもりA 100 gをバネ秤に吊るす (下画像①)
• 初期状態でバネ秤の目盛 200 gまで引っ張る。(プリロードを掛ける) → 初期軸力に相当 (下画像②)

現在の目盛りが200 gなので、100 gおもりを追加したらバネ秤の耐荷重に達して壊れてしまうのでしょうか？

答えは否です。

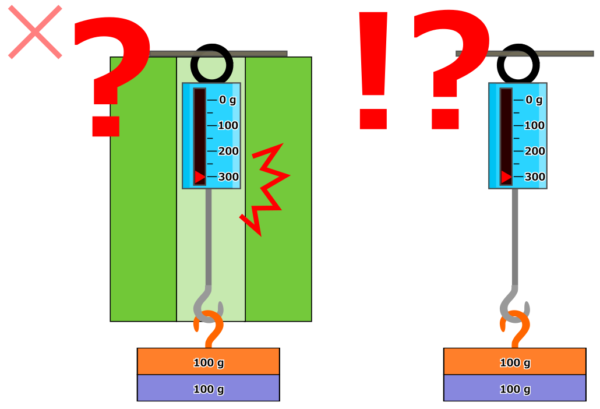
仮に壊れるのだとしたら、下の画像のように矛盾した状態になってしまいますよね。

• 追加100 gのおもりでバネ秤の耐荷重の300 gに達する。
• この状態で、特に役に立ってない緑の物体を消してみると･･･
• 200 gのおもりしか吊るしてないのにバネ秤の目盛りは300 gというミラクルな状態に！

これは誰が見ても間違っています。

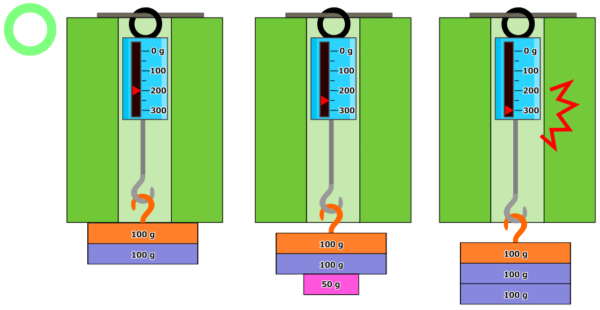
実際は、初期状態で200 gのプリロードがかかっているため、おもりを追加して合計が200 gを超えるまではバネ秤の目盛りは増えません。
そしてバネ秤が壊れるのは、追加のおもりが200gとなり、合計300 gのおもりを吊るしたときです。

初期の軸力 200 gでしたが、初期状態 + 200 g(合計300 gのおもり)で壊れることになります。
これは、初期のプリロード(=軸力)が150 gや250 gだった場合も同じく、合計300 gのおもりで壊れることになり、初期軸力と引張の外力は合算されないことがわかりますよね。

詳しくは「締付け線図」で検索を

今回の内容をよりアカデミックに説明しようとすると「締付け線図」によって表されます。
ボルトを引っ張る荷重と、ボルトが受ける荷重の比を「内外力比」とか言うんですが、具体的な数値がいくらなのかを知るのは難しく、機械設計の現場ではそんなに有用ではない感じです。

理論として存在するけど、実際に計算して設計の役に立てるのは難しそう。
考え方として勉強するのはアリだと思います。

まとめ

というわけで、ボルトが破断する時点では｢軸力と外力は加算されない｣ことがお分かりいただけたでしょうか。
安心して規定のトルクでボルトを締め付けて貰えればと思います。

 - 材料力学