せん断応力による滑り変形量(ひずみ)の計算方法

部材にせん断荷重がかかった時のせん断ひずみにより、どれくらい滑り変形するのか？
その計算方法について説明したいと思います。

とは言え機械設計において、せん断応力による滑り変形量を計算する事は、はっきり言ってほとんど無いかもしれません。
せん断ひずみによる滑り変形量はとても微小なものになり、さらに荷重をかけると大きく変形する前に破断するからです。

実用性はさておき、計算方法を知識として持っていても損はないかと思います。

変形量ではなく、どれだけのせん断荷重に耐えられるか？については下記の記事が参考になります。

せん断による滑り変形とは？

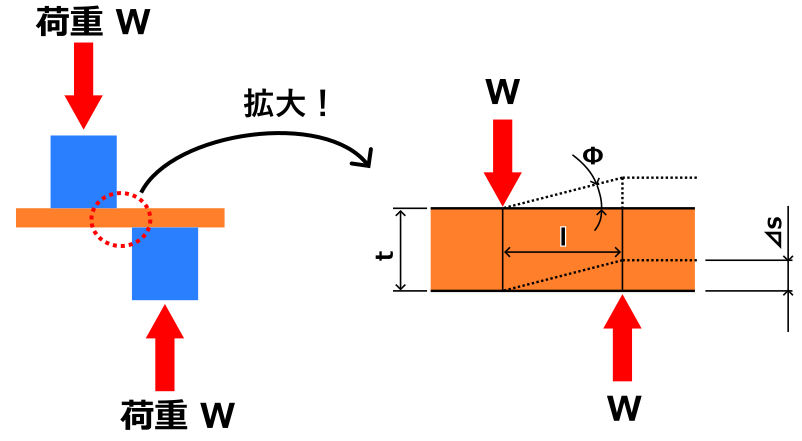
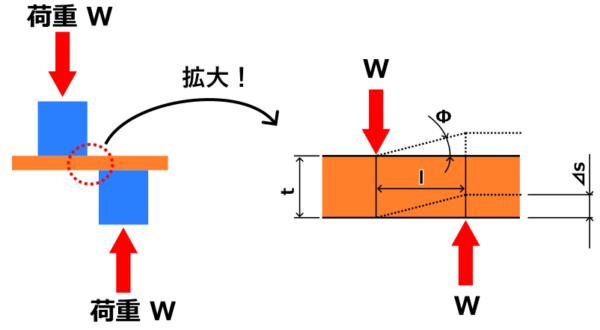
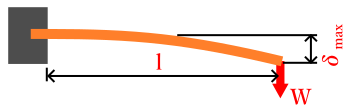
そもそも滑り変形って何？って思うかもしれませんが、まずは下の図をご覧ください。

このようにせん断荷重を部材にかけるといずれは破断しますが、破断する前の状態は右側の拡大図のように部材の一部が平行四辺形に変形します。
このときの⊿sが滑り変形量となります。

今回はこの滑り変形が何mmなのかを計算していきたいと思います。

例題

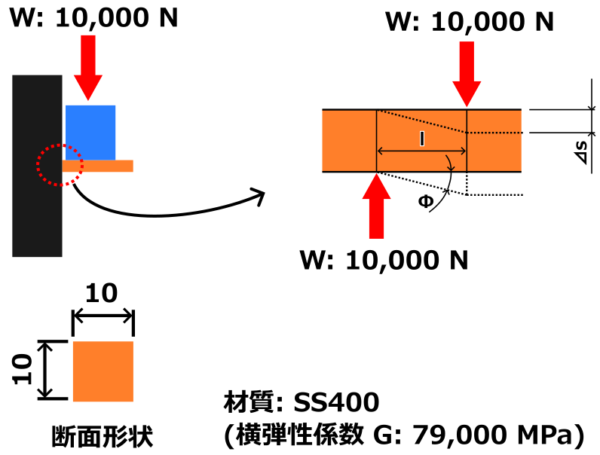
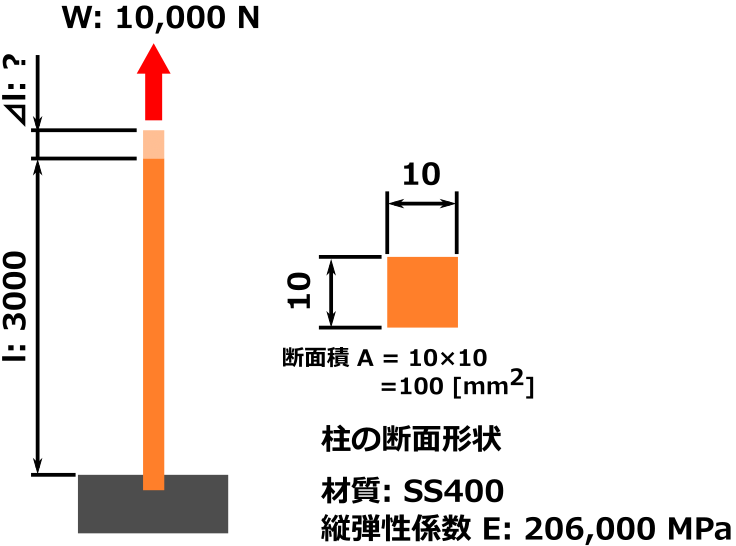
下の図のような状況の時の、せん断荷重による滑り変形量はいくらになるでしょうか？

条件

• 柱の断面積断面積: 100 mm²
• 荷重 10,000 N
• 距離 1 mm
• 横弾性係数 79,000 MPa

部材は壁に固定されているので、上からの荷重とともに壁の反力として下からも同じ荷重を受けていることになります。
[mntyzer_topmedium]

せん断応力による滑り変形量(ひずみ)計算の概要

せん断荷重から滑り変形量を求めるには、次のステップで計算出来ます。

1. 荷重と断面積から応力を求める
2. 応力と横弾性係数よりせん断ひずみを求める
3. せん断ひずみと距離より滑り変形量を求める

では、計算方法の詳細を説明します。
例題はその後で実際に計算してみましょう。

せん断応力による滑り変形量(ひずみ)計算の詳細

では、せん断荷重による滑り変形の計算方法を詳しく説明します。

荷重と断面積から応力を求める

部材をせん断する荷重が加わると、部材内部に「せん断応力」が発生します。
まずはこの「せん断応力」を求めます。

断面積が不明な場合は、部材のサイズよりまず断面積を計算してください。

応力と横弾性係数よりせん断ひずみを求める

次に「せん断ひずみ」を計算します。
せん断ひずみとは、せん断荷重が加えられた部材が変形している度合いを表します。
せん断ひずみは先程計算したせん断応力 τを材料の横弾性係数で割ることで求められます。

【参考】材料ごとの横弾性係数

弾性係数とは、応力とひずみが比例関係にある時の定数となります。
簡単に言えば、弾性係数の値が大きいほど荷重を加えても変形しにくい材料になります。

弾性係数は引張や圧縮に対応する「縦弾性係数」とせん断に対応する「横弾性係数」があり、材料ごとにある程度値が決まっています。

いくつかの材料の横弾性係数を下記に示しますので、参考にしてください。

※熱処理条件等により数値が大きく変動することがあります。正確な値は規格等で確認してください。
※樹脂材料の縦弾性係数は引張弾性率を記載
※樹脂材料の横弾性係数は縦弾性係数の40%とした場合の目安

材質	横弾性係数 G [MPa (N/mm2)]
軟鋼(SS400)	79,000
鋼(SCM435)	83,000
ステンレス(SUS304)	74,000
リン青銅(C5191)	40,000
アルミニウム(A5052)	26,000
銅(C1100)	44,000
樹脂(ABS)	1,220
樹脂(PP)	600
樹脂(PE)	400
樹脂(PMMA)	1,320
樹脂(POM)	940
樹脂(PC)	960
樹脂(PA66)	1,200

せん断ひずみと距離より滑り変形量を求める

せん断ひずみが求められたので、いよいよ滑り変形量を計算します。
滑り変形は、せん断ひずみともとの長さを掛け算したら計算できます。

計算式を見て分かるように、せん断荷重がかかる距離が長くなるほど滑り変形量が大きくなることがわかります。
ただし、この距離が長くなるとせん断による滑り変形よりも、曲げによるたわみの影響が大きくなり、計算結果と現実のズレが大きくなります。

この計算は、あくまでせん断による滑りのみを計算していることを忘れないようにしましょう。

せん断応力による滑り変形量の計算は以上です。

例題を計算してみる

では、例題を計算してみましょう。

荷重と断面積から応力を求める

まず部材内に発生するせん断応力ですが、式に代入するパラメータは下記になります。

W	10,000 [N]
A	100 [mm2]

値を式に入れて計算すると、せん断応力は100 MPaとなりました。

応力と横弾性係数よりせん断ひずみを求める

次にひずみを計算します。
材質は軟鋼という設定なので、横断線係数が79,000 MPaとなります。
式に代入するパラメータは下記。

τ(タウ)	100 [MPa]
G	79,000 [MPa]

式に代入すると、せん断ひずみは0.00127 radとなりました。

せん断ひずみと距離より滑り変形量を求める

最後に滑り変形量を求めます。
代入するパラメータは下記です。

γ(ガンマ)	0.00127[rad]
l	1 [mm]

式に代入して計算します。
距離が1 mmなので、もはや計算する必要も無い雰囲気ですが…

というわけで滑り変形量は0.00127 mmになることが分かりました！

約1/1000 mmと、かなり微小な変形量ですね。
測定してもほとんど分からないでしょう。
微小すぎて、計算する意味があまりないことも理解していただけたと思います。

計算できる範囲は比例限度まで

例題の計算結果は0.00127 mmの変形と、とても小さな値でした。
では荷重をどんどん大きくしていったらもっと変形する？と思いますが、変形量を正確に計算することが難しくなります。
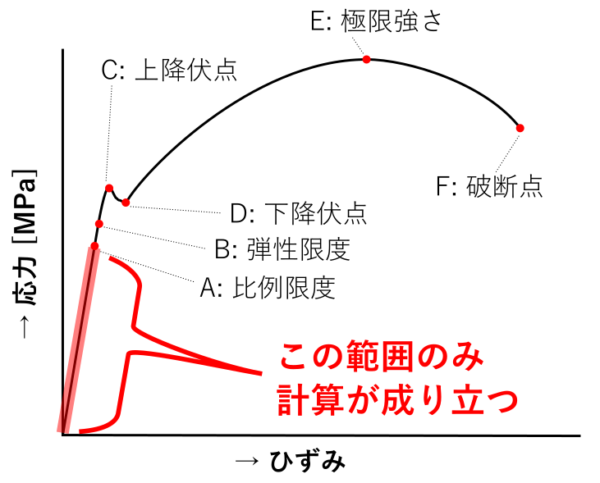
材料の降伏点を超えると応力に対する変形量(ひずみ)一気に大きくなり、さらに大きな荷重では材料が破断してしまうからです。

計算に「横弾性係数 G」を使っていることから分かるように、この計算はフックの法則が成り立つ範囲にのみ成立します。
応力ひずみ線図で言うと、比例限度までとなります。
ただし各材料の比例限度がいくら、というデータは手に入りづらいので、「だいたい降伏点以下なら成り立つ」と考えておいて大きな問題はありません。

ちなみにせん断に対する極限強さ、降伏応力は、引張に対する極限強さ、降伏応力の60%程度となります。

まとめ

せん断荷重から滑り変形量を求めるには、次のステップで計算出来ます。

1. 荷重と断面積から応力を求める
2. 応力と横弾性係数よりせん断ひずみを求める
3. せん断ひずみと距離より滑り変形量を求める

ただし滑り変形量は微小なため、機械設計において計算する機会はあまりないかもしれません。